Задача №115185. Разноцветный граф
Дан неориентированный граф на \(n\) вершинах, содержащий \(m\) ребер, пронумерованных от \(1\) до \(m\). Каждое ребро покрашено в один из \(k\) цветов. \(i\)-е ребро соединяет вершины \(v_i\) и \(u_i\) и имеет цвет \(c_i\).
Назовём граф хорошим , если в нём можно оставить ровно \(n-1\) ребро так, чтобы граф был связным и среди оставленных ребер было хотя-бы одно ребро каждого цвета.
Дано \(q\) изменений цветов ребер графа. Каждое изменение задаётся двумя числами \(e_i\) и \(w_i\) и означает, что цвет \(e_i\)-го ребра становится равным \(w_i\). После каждого изменения графа определите, является ли он хорошим .
В первой строке находятся три целых числа \(n\), \(m\) и \(k\) (\(2 \leq n \leq 100\,000\), \(1 \leq m \leq 100\,000\), \(1 \leq k \leq 8\)) — количество вершин, рёбер и цветов соответственно.
Следующие \(m\) строк содержат описание рёбер. \(i\)-я из них содержит три числа \(v_{i}\), \(u_{i}\) и \(c_{i}\) (\(1 \leq v_{i}, u_{i} \leq n\), \(1 \leq c_{i} \leq k\), \(v_i \neq u_i\)) — концы \(i\)-го ребра и его цвет соответственно.
Следующая строка содержит единственное целое число \(q\) (\(1 \leq q \leq 100\,000\)) — количество изменений.
Следующие \(q\) строк содержат описание изменений. \(i\)-я из них содержит два целых числа \(e_{i}\) и \(w_{i}\) (\(1 \leq e_{i} \leq m\), \(1 \leq w_{i} \leq k\)) — номер ребра и его новый цвет.
Гарантируется, что в графе нет петель и кратных ребер.
В \(i\)-й строке выведите « Yes » (без кавычек), если граф после \(i\)-го запроса хороший , и « No » (без кавычек) иначе.
В первом примере после первого изменения граф выглядит так:
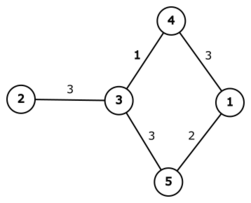
В этом случае нет ни одного ребра цвета \(1\), поэтому условие задачи не может быть выполнено.
После второго изменения граф выглядит так:
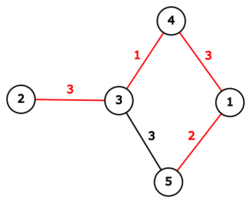
Красным выделены рёбра, которые можно оставить. В данном случае, они подходят, так как среди них есть все цвета \(1\), \(2\) и \(3\), а так же они образуют связный граф.
Тесты к этой задаче состоят из 8 групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
| Доп. ограничения | ||||
| Группа | Баллы | \(k\) | Необх. группы | Комментарий |
| 0 | 0 | – | – | Тесты из условия. |
| 1 | 10 | \(k \le 1\) | – | |
| 2 | 9 | \(k \le 2\) | \(1\) | |
| 3 | 15 | \(k \le 3\) | \(0\) – \(2\) | |
| 4 | 16 | \(k \le 4\) | \(0\) – \(3\) | |
| 5 | 14 | \(k \le 5\) | \(0\) – \(4\) | |
| 6 | 13 | \(k \le 6\) | \(0\) – \(5\) | |
| 7 | 12 | \(k \le 7\) | \(0\) – \(6\) | |
| 8 | 11 | \(k \le 8\) | \(0\) – \(7\) | Offline-проверка. |
5 5 3 3 4 1 1 5 2 3 2 3 1 4 3 3 5 3 5 1 3 4 1 5 1 2 1 3 2
No Yes Yes No Yes
2 1 1 1 2 1 1 1 1
Yes