Открытая олимпиада школьников по программированию

Задача №115186. Турнир

Это интерактивная задача.

Загадан турнирный граф на $n$ вершинах, пронумерованных от $1$ до $n$. Турнирный граф — это ориентированный граф, в котором любое ребро соединяет две различные вершины, причём для любой пары различных вершин $u$ и $v$ есть ровно одно ребро, ориентированное либо от $u$ к $v$, либо от $v$ к $u$.

Вам известно лишь количество вершин в графе, за один запрос вы можете узнать в какую сторону направлено ребро между любой парой вершин.

Назовём вершину хорошей , если из неё исходит не более одного ребра. Ваша задача найти любую хорошую вершину, либо определить что таких вершин нет, сделав не более $2000$ запросов.

Протокол взаимодействия

Ваша программа будет взаимодействовать с программой жюри с использованием стандартных потоков ввода и вывода. Каждое взаимодействие будет состоять из решения задачи для нескольких наборов входных данных.

Сначала ваша программа должна считать два целых числа $g$ и $t$ ($0 \le g \le 10$, $1 \le t \le 100$) — номер группы тестов и количество наборов входных данных в рамках одного взаимодействия с программой жюри. Затем $t$ раз необходимо выполнить взаимодействие по решению задачи для набора входных данных.

Рассмотрим протокол взаимодействия для одного набора входных данных.

Сначала ваша программа должна считать одно число $n$ ($1 \le n \le 500$) — количество вершин загаданного графа.

После этого вы можете задавать запросы. Для одного запроса выведите « ? u v » ($1 \le u, v \le n$, $u \neq v$). В ответ на это программа жюри в единственное строке выведет « forward », если ребро направлено от $u$ к $v$ и « backward », если ребро направлено от $v$ к $u$. Для каждого набора входных данных вы можете задать не более $2000$ запросов.

Чтобы вывести ответ, выведите « ! u » ($1 \le u \le n$ или $u = -1$), где $u$ — номер хорошей вершины, или $-1$, если такой вершины нет. Если выведенный ответ верный, то программа жюри выведет « OK », после этого ваша программа должна сразу перейти к обработке следующего набора входных данных или завершится, если это был последний граф. В ином случае программа жюри выведет « WRONG ». При считывании этой строки ваша программа должна немедленно завершить свое исполнение.

Обратите внимание, что ограничения на $n$ даны для каждого набора входных данных, дополнительных ограничений на сумму $n$ по всем наборам входных данных нет.

Если вы используете « cout « ... « endl » в C++, « System.out.println » в Java, « print » в Python, « writeln » в Pascal, то сброс потока вывода происходит автоматически, дополнительно ничего делать не требуется.

Если вы используете другой способ вывода, рекомендуется делать сброс буфера потока вывода. Обратите внимание, что перевод строки надо выводить в любом случае. Для сброса буфера потока вывода можно использовать « fflush(stdout) » в С++, « flush(output) » в Pascal, « System.out.flush() » в Java, « sys.stdout.flush() » в Python.

Примеры

Входные данные

0 2
3

forward

backward

OK
5

forward

forward

backward

backward

forward

forward

backward

forward

forward

forward

OK

Выходные данные

Примечание

В первом тестовом примере, так как программа жюри неадаптивна, граф загадан заранее и имеет следующий вид:

$\text{[math]}$

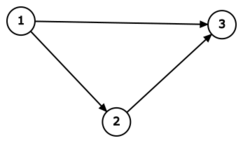
Поэтому на запрос « ? $1$ $2$» программа жюри вывела « forward », так как ребро направлено от $1$ к $2$, а на запрос « ? $3$ $2$» программа жюри вывела « backward », так как ребро направлено от $2$ к $3$. В этом случае вершины $2$ и $3$ являются хорошими , а вершина $1$ нет. Поэтому на ответ « ! $3$» программа жюри вывела « OK ».

Во втором тестовом примере из каждой вершины исходит больше одно ребра, поэтому на ответ « ! $-1$» программа жюри вывела « OK ».

Система оценки

Тесты к этой задаче состоят из 10 групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.

В данной задаче программа жюри может действовать двумя способами:

Неадаптивно. То есть структура графа фиксируется заранее и не подстраивается под запросы.
Адаптивно. То есть структура графа может меняться во время взаимодействия. При этом гарантируется, что всегда существует хотя бы один граф, который подходит под ответы на все уже заданные запросы. В этом случае, ответ вашего решения будет признан корректным, только если он будет верен для всех подходящих графов.

		Доп. ограничения
Группа	Баллы	$n$	Программа жюри	Необх. группы	Комментарий
0	0	–	Неадаптивна	–	Тесты из условия.
1	14	$n \le 63$	Адаптивна	0
2	8	–	Адаптивна	–	Граф является особым $^1$
3	11	–	Адаптивна	–	Граф является особым $^2$
4	12	–	Адаптивна	–	Граф является особым $^3$
5	9	$n \le 100$	Адаптивна	0, 1
6	10	$n \le 400$	Неадаптивна	0
7	9	$n \le 400$	Адаптивна	0, 1, 5, 6
8	8	$n \le 450$	Неадаптивна	0, 6
9	10	–	Неадаптивна	0, 6, 8
10	9	–	Адаптивна	0 – 9	Offline-проверка.

$^1$ Граф называется особым $^1$, если существует перестановка вершин $v_1$, $v_2$, $\ldots$, $v_n$, что для любых $i < j$ верно, что ребро ориентированно от вершины $v_i$ к вершине $v_j$.

$^2$ Граф называется особым $^2$, если для любой вершины с номером $v > 2$, ребро ориентировано от нее к вершине 1 или к вершине 2, или к обеим вершинам 1 и 2.

$^3$ Граф называется особым $^3$, если $n \ge 4$ и существует перестановка вершин $v_1$, $v_2$, $\ldots$, $v_n$, что ребро $(v_i, v_{i+1})$ ориентированно от $v_i$ к $v_{i+1}$, а любое другое ребро $(v_i, v_j)$ ($i + 1 < j$) ориентировано от $v_j$ к $v_i$.

Сдать: для сдачи задач необходимо войти в систему