Задача №115188. Обед

Дан выпуклый многоугольник из $N$ точек. Не гарантируется , что никакие три из них не лежат на одной прямой. В многоугольнике даны $M$ различных особых точек. Также дана точка $C$ с координатами $(x_0, y_0)$, лежащая внутри данного выпуклого многоугольника, но не на его границе.

Алиса и Боб играют в игру, делая ходы по очереди, начиная с Алисы. На очередном ходу, игрок должен выбрать вершину многоугольника отличную от $C$ и переместить её в точку $C$. Если в многоугольнике уже есть вершина в точке $C$, то эти вершины объединяются. Ход можно совершить только в случае, если существует особая точка, лежащая в многоугольнике до хода, но не лежащая в нём после. Гарантируется, что точка никогда не может оказаться на границе многоугольника после любого количества ходов.

После хода многоугольник не обязан быть выпуклым, а так же может стать вырожденным (то есть стать отрезком). Проигрывает тот, кто не может сделать ход.

Также есть $q$ изменений двух видов:

$+ \ x \ y$, что означает, что точка с координатами $(x, y)$ становится особой . Гарантируется, что до этого эта точка не была особой .
$- \ x \ y$, что означает, что точка с координатами $(x, y)$ перестаёт быть особой . Гарантируется, что до этого эта точка была особой .

После каждого изменения, а также в самом начале, определите, какой игрок должен победить при оптимальной игре обоих. После каждого изменения игра начинается с исходного многоугольника, с учетом примененных изменений к особым точкам.

Входные данные

Первая строка содержит три целых числа $n$, $m$ и $q$ ($3 \le n \le 10\,000$, $0 \le m \le 100\,000$, $0 \le q \le 1\,000\,000$) — количество точек в многоугольнике, количество особых точек и количество изменений.

Вторая строка содержит два целых числа $x_0$ и $y_0$ ($-10^9 \le x_0, y_0 \le 10^9$) — координаты точки $C$. Гарантируется, что точка лежит внутри данного многоугольника и не лежит на его границе.

Следующие $n$ строк содержат по два целых числа $x_i$ и $y_i$ ($-10^9 \le x_i, y_i \le 10^9$) — координаты $i$-й точки многоугольника. Точки вводятся в порядке обхода против часовой стрелки.

Следующие $m$ строк содержат по два целых числа $x_i$ и $y_i$ ($-10^9 \le x_i, y_i \le 10^9$) — координаты $i$-й особой точки. Гарантируется, что в любой момент времени точки различны и лежат внутри многоугольника.

Следующие $q$ строк содержат описание запросов. В $i$-й из них находится символ $c$ и два целых числа $x$ и $y$ ($c =$ « + » или « - » (без кавычек), $-10^9 \le x, y \le 10^9$) — описание очередного запроса.

Если $c =$ « + », то точка $(x, y)$ становится особой . Гарантируется, что до этого эта точка не была особой .
Если $c =$ « - », то точка $(x, y)$ перестаёт быть особой . Гарантируется, что до этого эта точка была особой .

Гарантируется, что в любой момент времени после любого количества корректных ходов никакая из особых точек не может оказаться на границе многоугольника.

Выходные данные

Выведите $q + 1$ строку. В первой строке выведите « Alice » (без кавычек), если до всех изменений при оптимальной игре побеждает Алиса, и « Bob » (без кавычек) иначе. Далее в $i$-й строке выведите победителя игры после $(i-1)$-го изменения в аналогичном формате.

Примечание

Рассмотрим многоугольник перед всеми изменениями:

$\text{[math]}$

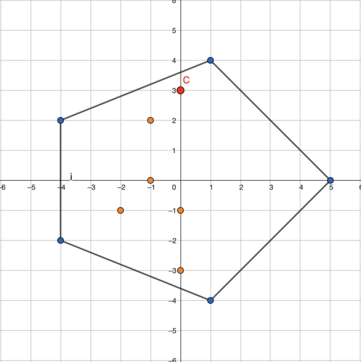
На первом ходу Алиса может передвинуть вершину многоугольника с координатами (-4; -2), тогда многоугольник будет выглядеть так:

$\text{[math]}$

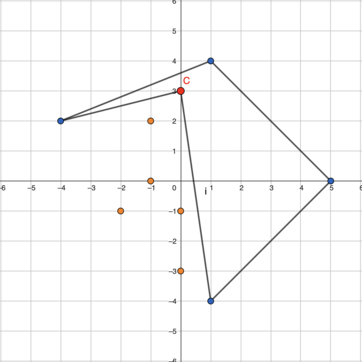
В этом состоянии многоугольника Боб уже не может сделать ход, а значит проигрывает.

Система оценки

Тесты к этой задаче состоят из 6 групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.

		Доп. ограничения
Группа	Баллы	$n$	$m$	$q$	Необх. группы	Комментарий
0	0	–	–	–	–	Тесты из условия.
1	16	$n = 3$	$m \le 3$	$q=0$	–
2	13	$n \le 18$	$m \le 18$	$q \le 1$	1
3	15	$n \le 18$	$m \le 18$	–	0 – 2
4	17	$n \le 5000$	$m \le 5000$	$q \le 1$	1, 2
5	21	$n \le 5000$	$m \le 100\,000$	$q \le 5000$	0 – 2, 4
6	18	–	–	–	0 – 5	Offline-проверка.

Примеры

Входные данные

Выходные данные

Alice
Bob
Bob
Bob

Сдать: для сдачи задач необходимо войти в систему