Задача №115189. Парные дороги
В некотором государстве есть \(n\) городов, между которыми пока что не построено ни одной дороги. В \(i\)-м городе живет \(w_i\) человек. Так же есть \(n - 1\) дорога, которую можно построить. \(i\)-я дорога при её строительстве соединит города \(u_i\) и \(v_i\), а стоимость её строительства равна \(s_i\).
Известно, что если построить все дороги, то от каждого города можно будет добраться до любого другого, используя только эти дороги. Другими словами, дороги образуют дерево.
В каждый из следующих \(k\) дней будет происходить следующее: В \(i\)-й день выбирается некоторый город \(c_i\), а также две различные ещё не построенные дороги, соединяющие этот город с какими-то другими городами. После этого эти две дороги строятся, за это платится цена, равная суммарной стоимости строительства этих двух дорог. Город \(c_i\) в этом случае является центральным в день \(i\).
Через \(k\) дней каждый город, являющийся центральным в хотя-бы один из \(k\) дней, принесёт ровно столько прибыли, сколько человек в нём живёт.
Выгодой назовём разность между прибылью, которую принесут города, и суммарной стоимостью построенных дорог. Найдите максимально возможную выгоду .
Первая строка содержит три целых числа \(n\), \(k\) и \(t\) (\(3 \le n \le 200\,000\), \(1 \le k \le \frac{n-1}2\), \(0 \le t \le 1\)) — количество городов, количество пар дорог, которые надо построить, а также число \(t\) равное \(1\), если нужно найти какие именно дороги надо построить, и равное \(0\) иначе.
Вторая строка содержит \(n\) целых чисел \(w_1\), \(w_2\), \(\ldots\), \(w_n\) (\(1 \le w_i \le 10^8\)) — количество жителей в городах.
Следующие \(n-1\) строк содержат по три целых числа \(u_i\), \(v_i\) и \(s_i\)(\(1 \le u_i, v_i \le n\), \(1 \le s_i \le 10^8\)) — номера городов, которые соединяет \(i\)-я дорога и стоимость её строительства.
Гарантируется, что дороги образуют дерево, и что можно построить \(k\) пар дорог, удовлетворяющих условию задачи.
В первой строке выведите единственное целое число — максимальную выгоду , которую можно получить после строительства ровно \(k\) пар дорог.
Если \(t = 1\), то в следующих \(k\) строках выведите \(k\) троек чисел \(c_i\), \(x_i\) и \(y_i\) (\(1 \le c_i, x_i, y_i \le n\)) — описание пар дорог, которые надо построить. Такая тройка задаёт пару из дороги \((c_i, x_i)\) и дороги \((c_i, y_i)\).
Если существует несколько способов получить максимальную выгоду , выведите любой из них.
В первом тесте из условия предлагается построить следующие дороги (одинаковым цветом отмечены дороги из одной пары):
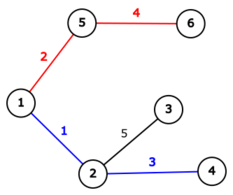
Суммарная стоимость строительства этих дорог равна \(2 + 4 + 1 + 3 = 10\). После строительства, города \(2\) и \(5\) принесут по \(2\) и \(5\) прибыли соответственно. Таким образом, выгода равна \(2 + 5 - 10 = -3\). Можно показать, что лучший ответ получить нельзя.
Во втором тесте из условия предлагается построить следующие дороги:
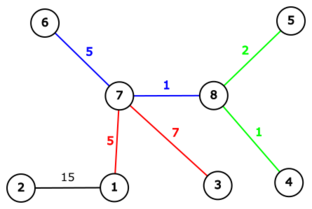
Суммарная стоимость строительства этих дорог равна \(5 + 1 + 2 + 1 + 5 + 7 = 21\). После строительства, города \(7\) и \(8\) принесут по \(3\) и \(5\) прибыли соответственно. Таким образом, выгода равна \(3 + 5 - 21 = -13\). Можно показать, что лучший ответ получить нельзя.
Тесты к этой задаче состоят из 7 групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
| Доп. ограничения | |||||
| Группа | Баллы | \(n\) | \(t\) | Необх. группы | Комментарий |
| 0 | 0 | – | – | – | Тесты из условия. |
| 1 | 13 | \(n \le 200\) | \(t = 0\) | – | |
| 2 | 17 | \(n \le 2000\) | \(t = 0\) | \(1\) | |
| 3 | 12 | \(n \le 2000\) | – | \(0\) – \(2\) | |
| 4 | 19 | – | \(t = 0\) | – | \(u_i = i\), \(v_i = i + 1\) |
| 5 | 11 | – | – | \(4\) | \(u_i = i\), \(v_i = i + 1\) |
| 6 | 15 | – | \(t = 0\) | \(1\), \(2\), \(4\) | Offline-проверка. |
| 7 | 13 | – | – | \(0\) – \(6\) | Offline-проверка. |
6 2 1 1 2 3 4 5 6 1 2 1 2 3 5 2 4 3 1 5 2 5 6 4
-3 5 6 1 2 4 1
8 3 0 4 5 1 2 3 1 3 5 2 1 15 7 1 5 4 8 1 8 5 2 7 8 1 6 7 5 3 7 7
-13