Задача №115196. Бурёнка и Pether

Однажды принцесса Бурляндии Бурёнка решила порадовать свою знакомую ReLu. Зная, что ReLu разделяет её интерес к криптовалюте, Бурёнка решила создать собственную блокчейн криптовалюту Pether .

Пройдя курсы и тренинги от эксперт-коуча по личностному росту в кибербезопастности, Бурёнка решила, что валюта Pether должна быть защищена наилучшим образом. В результате, из-за невероятно сложных и запутанных ограничений, далеко не все пользователи могут обмениваться Pether друг с другом.

Устройство блокчейн валюты Pether действительно сложное и запутанное. Все пользователи пронумерованы целыми числами от $1$ до $n$. Каждому пользователю присвоен его уникальный идентификатор $a_{i}$. Также для валюты зафиксировано число $d$ — параметр безопасности.

Пользователь $i$ может напрямую перевести валюту пользователю $j$, только если $i < j$ и $a_i < a_j$. Но и этого недостаточно! Прямой перевод валюты между пользователями происходит посредством цепочки транзакций через некоторое число промежуточных пользователей. За время каждой транзакции номер каждого следующего промежуточного пользователя (включая последнего пользователя $j$) должен увеличиваться, но не более, чем на $d$. Также все промежуточные пользователи кроме $i$ и $j$ должны иметь идентификатор строго меньше $a_i$.

Более формально, пользователь $i$ может напрямую перевести криптовалюту пользователю $j$, если выполнены следующие условия:

Выполнено, что $i < j$
Выполнено, что $a_{i} < a_{j}$
Существует последовательность промежуточных пользователей $x$ длины $k$ такая что:
1. $i = x_1 < x_2 < \ldots < x_{k-1} < x_{k} = j$
2. Для всех $1 \le t \le k - 1$ верно, что $x_{t + 1} - x_{t} \le d$
3. Для всех $2 \le t \le k - 1$ верно, что $a_{x_t} < a_{i}$

Буренка просит вас, своего знакомого программиста, разобраться в этой системе и выяснить для некоторых пар пользователей, как им передавать Pether друг другу.

Вам нужно ответить на $q$ запросов. В каждом запросе вам требуется определить, существует ли последовательность прямых переводов валют (возможно через промежуточных пользователей), позволяющая передать Pether от пользователя $u_i$ к пользователю $v_i$. В некоторых запросах также требуется минимизировать число прямых переводов валют в процессе отправки валюты от $u_i$ к $v_i$. Обратите внимание, что число транзакций во время каждого прямого перевода минимизировать не требуется.

Входные данные

В первой строке даны три целых числа $n$, $d$ и $g$ $(1 \leq n, d \leq 300\,000, 0 \leq g \leq 12)$ — количество пользователей, параметр безопасности и номер группы тестов.

Во второй строке даны $n$ целых чисел $a_1,\ a_2,\ \ldots,\ a_n$ $(1 \leq a_{i} \leq n)$ — идентификаторы пользователей. Гарантируется, что все числа $a_i$ различны .

В третьей строке находится единственное целое число $q$ $(1 \leq q \leq 300\,000)$ — количество запросов

В следующих $q$ строках дано по три целых числа $t_{i},\ u_{i},\ v_{i}$ $(t_{i}\in \{1, 2\}, 1 \leq u_{i} < v_{i} \leq n)$, где $u_i$ — пользователь, который должен отдать валюту, $v_i$ — пользователь, который должен получить валюту. Если $t_i = 1$, то необходимо выяснить, возможно ли передать валюту, а если $t_i = 2$, то надо дополнительно минимизировать число прямых переводов.

Выходные данные

Выведите $q$ строк, в $i$-й из них должен быть ответ на $i$-й запрос.

Если передать валюту от пользователя $u_i$ к пользователю $v_i$ нельзя, то в ответ на $i$-й запрос выведите 0. Иначе, если $t_i = 1$, то выведите 1, а если $t_i = 2$, то выведите минимальное число прямых переводов, требуемых для передачи Pether от $u_i$ к $v_i$.

Примечание

В первом примере возможны следующие прямые переводы между пользователями:

$\text{[math]}$

В первом запросе пользователь с индексом $1$ может напрямую перевести Pether пользователю с индексом $3$, сделав 2 транзакции через промежуточного пользователя 2.

Во втором запросе прямой перевод между пользователями с индексами $1$ и $2$ невозможен, так как $a_{1} = 2 > a_{2} = 1$.

В третьем запросе можно перевести валюту от пользователя $1$ к пользователю $4$ с помощью двух прямых переводов, в начале переведя валюту от пользователя $1$ к пользователю $3$, а потом от $3$ к $4$. Так как $t_3 = 1$, то требуется узнать лишь наличие возможности передачи валюты, поэтому ответ на запрос равен 1.

В четвертом запросе можно обойтись тремя прямыми переводами: от $1$ к $3$, от $3$ к $4$ и от $4$ к $5$.

Во втором примере возможны следующие прямые переводы между пользователями:

$\text{[math]}$

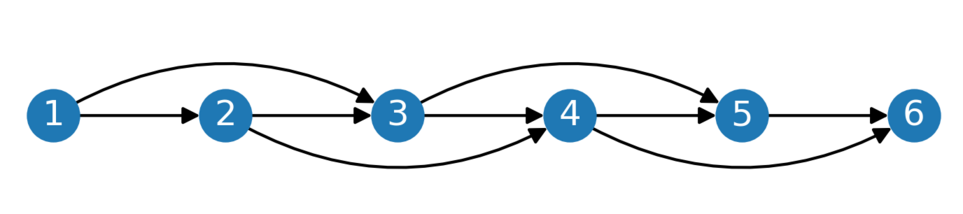
В третьем примере возможны следующие прямые переводы между пользователями:

$\text{[math]}$

Система оценки

Тесты к этой задаче состоят из двенадцати групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.

		Доп. ограничения
Группа	Баллы	$n$	$q$	$v_i, a_{n}, t_i$	Необх. группы	Комментарий
0	0	–	–	–	–	Тесты из условия.
1	10	$n \le 100$	$q \le 100$	–	–
2	7	$n \le 1000$	–	–	1
3	14	–	–	$a_{n} = n, v_{i} = n$	–
4	10	–	$q = 1$	$v_i = n$	–
5	9	–	–	$v_i = n$	3, 4
6	7	–	–	$t_i=2$	–	Ответ не превосходит $10$
7	7	–	–	$t_i=2$	1, 6	Ответ не превосходит $150$
8	13	–	–	$t_i = 1$	–
9	10	$n \le 50\,000$	$q \le 50\,000$	–	1
10	4	$n \le 100\,000$	$q \le 100\,000$	–	1, 9
11	4	$n \le 200\,000$	$q \le 200\,000$	–	1, 9, 10
12	5	–	–	–	0 – 11	Offline-проверка.

Примеры

Входные данные

6 1 0
2 1 3 4 5 6
6
2 1 3
2 1 2
1 1 4
2 1 5
2 1 6
1 2 6

Выходные данные

Входные данные

6 2 0
1 2 3 4 5 6
6
2 1 5
2 2 5
2 1 6
2 2 6
2 1 4
2 2 4

Выходные данные

Входные данные

10 2 0
2 1 4 3 5 6 8 7 10 9
10
2 1 5
1 2 5
2 3 5
2 1 9
2 5 8
2 3 9
2 1 8
1 1 2
2 3 8
2 1 9

Выходные данные

Сдать: для сдачи задач необходимо войти в систему