Задача №115225. Улитка на склоне
Тихо взобравшись на вершину горы Фудзи, улитка хочет спуститься вниз. На склоне горы находится система тропинок, образующая подвешенное двоичное дерево.
Дерево содержит \(n\) вершин, соединенных \(n-1\) тропинками. На вершине горы находится корень дерева. В некоторых вершинах тропинка заканчивается, они являются листами дерева. От каждой вершины, кроме листьев, вниз по склону отходят ровно две тропинки, одна ведет налево, а другая — направо.
Улитка хочет, начав в корне, спуститься по дереву и добраться до одного из листьев. Она будет спускаться, перемещаясь вниз по тропинкам. В каждой вершине по пути улитка может выбрать одно из двух направлений дальнейшего спуска: налево или направо.
Улитка может начать спуск в корне в любом из двух направлений. В каждой из последующих вершин улитка делает поворот , если она выбрала направление, отличающееся от выбранного в предыдущей вершине.
Улитке неудобно поворачивать, поэтому на всем пути от корня до листа улитка готова сделать не более \(k\) поворотов.
Пронумеруем вершины дерева от \(1\) до \(n\), при этом корень получит номер \(1\). Вам дано \(q\) запросов. Каждый запрос описывается одной вершиной \(u_i\). Требуется найти количество листьев, в которых улитка сможет завершить свой спуск, если она будет спускаться из корня, сделает не более \(k\) поворотов, и по пути пройдет через вершину \(u_i\).
В первой строке даны три целых числа \(n\), \(k\) и \(q\) — количество вершин в дереве, максимальное количество поворотов, которое улитка готова сделать, и количество запросов (\(3 \le n \le 200\,000\); \(0 \le k \le n\); \(1 \le q \le 200\,000\)).
В следующих \(n\) строках дано описание дерева. Первым в \(i\)-й строке дано целое число \(t_i\) — количество тропинок, выходящих из \(i\)-й вершины (\(t_i = 0\) или \(t_i = 2\)). Если \(t_i = 2\), то далее в той же строке даны два целых числа \(l_i\) и \(r_i\) — номера вершин, в которые ведёт соответственно левая и правая тропинка из вершины \(i\) (\(1 \le l_i, r_i \le n\)). Гарантируется, что это описание соответствует подвешенному двоичному дереву с корнем в вершине \(1\).
В следующих \(q\) строках даны запросы. В \(i\)-й строке дано одно целое число \(u_i\) — номер вершины, через которую должна пройти улитка на своем пути (\(1 \le u_i \le n\)).
Для каждого запроса, выведите ответ на него в новой строке — количество листьев, в которых улитка может завершить свой маршрут, если она начинает в корне, спускается вниз, на своем пути совершает не больше \(k\) поворотов и проходит через вершину \(u_i\).
| Подзадача | Баллы | Дополнительные ограничения | Необх. подзадачи |
| 1 | 11 | \(n \le 500\), \(q \le 500\) Во всех запросах \(u_i\) является листом | |
| 2 | 12 | \(n \le 500\), \(q \le 500\) | У, 1 |
| 3 | 10 | \(k = n\) | |
| 4 | 14 | \(k = 0\) | |
| 5 | 19 | Во всех запросах \(u_i\) является листом | 1 |
| 6 | 34 | Без дополнительных ограничений | У, 1–5 |
|
|
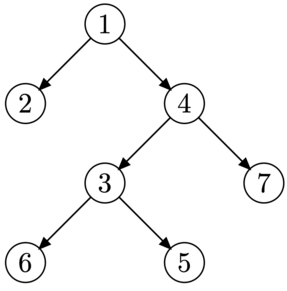
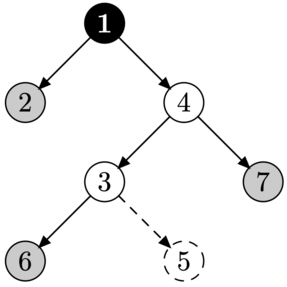
| Структура дерева в тесте из примера. | Улитка должна пройти через вершину \(1\), она может завершить путь в листах \(2\), \(6\) и \(7\). |
|
|
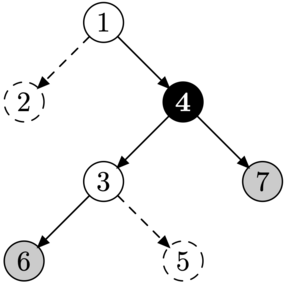
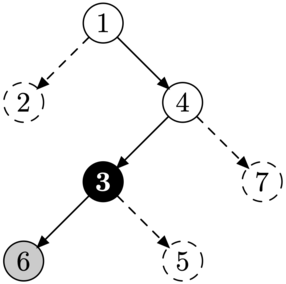
| Улитка должна пройти через \(4\), она может завершить путь в \(6\) и \(7\). | Улитка должна пройти через \(3\), она может завершить путь только в листе \(6\). |
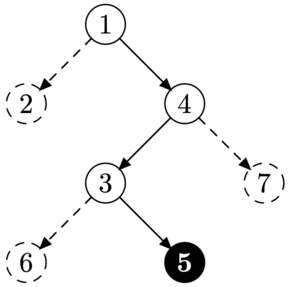Улитка должна пройти через \(5\), однако путь до этой вершины уже содержит больше одного поворота. Поэтому не существует листа, в котором улитка могла бы завершить путь, выполнив все ограничения.
7 1 4 2 2 4 0 2 6 5 2 3 7 0 0 0 1 4 3 5
3 2 1 0