Задача №115226. Конференция
Тюменская Ассоциация Научных и Образовательных Сообществ организует конференцию, в рамках которой планировалось провести \(n\) мероприятий, пронумерованных от \(1\) до \(n\). При этом \(i\)-е мероприятие задаётся двумя целыми числами \(l_i\) и \(r_i\) — временем начала и окончания мероприятия.
Поскольку некоторые мероприятия могут перекрываться или даже полностью совпадать по времени, один человек не всегда может посетить все мероприятия конференции. Будем считать, что мероприятия \(i\) и \(j\) не пересекаются, если \(r_i < l_j\) или \(r_j < l_i\).
Будем называть множество мероприятий совместным , если любые два различных мероприятия в этом множестве не пересекаются. Пусть максимальный размер совместного множества мероприятий на конференции равен \(m\). Будем называть насыщенностью конференции отношение \(n/m\).
В связи с сокращением финансирования, организаторы конференции приняли решение, что число мероприятий на конференции будет уменьшено ровно в два раза. При этом они хотят сохранить насыщенность конференции неизменной, поэтому максимальный размер совместного множества мероприятий в рамках конференции также должен уменьшиться ровно в два раза. Удачным образом оказалось, что в исходном плане конференции как количество мероприятий \(n\), так и максимальное возможное количество мероприятий в совместном множестве \(m\) — чётные числа.
Помогите организаторам выбрать множество из \(n/2\) исходно запланированных мероприятий, которые необходимо провести, чтобы при этом размер максимального совместного множества выбранных мероприятий оказался равен \(m/2\).
Один тест содержит несколько наборов входных данных.
В первой строке дано одно целое число \(t\) — количество наборов входных данных (\(1 \le t \le 50\,000\)).
В первой строке каждого описания набора дано одно целое число \(n\) — количество мероприятий в исходном плане (\(2 \le n \le 100\,000\), \(n\) — чётное).
В следующих \(n\) строках каждого описания набора дано описание мероприятий. В \(i\)-й строке даны два целых числа \(l_i\) и \(r_i\) — время начала и конца \(i\)-го мероприятия (\(1 \le l_i < r_i \le 10^9\)).
Гарантируется, что \(m\) — размер максимального совместного множества мероприятий для исходного плана, чётно.
Для каждого набора входных данных выведите в новой строке \(n/2\) различных номеров мероприятий, которые необходимо провести. Если существует несколько подходящих ответов, вы можете вывести любой из них. Для проведенных мероприятий размер максимального совместного множества мероприятий должен быть равен \(m/2\).
Обозначим сумму \(n\) по всем наборам входных данных в одном тесте как \(N\).
Будем говорить, что мероприятие \(i\) накрывает мероприятие \(j\), если \(l_i \le l_j < r_j \le r_i\).
| Ограничения | ||||
| Подз. | Баллы | \(N\) | Дополнительные ограничения | Необх. подзадачи |
| 1 | 5 | \(N \le 100\,000\) | Любые два мероприятия не пересекаются | |
| 2 | 20 | \(N \le 20\) | У | |
| 3 | 7 | \(N \le 30\) | У, 2 | |
| 4 | 15 | \(N \le 500\) | В каждой паре мероприятий либо одно мероприятие накрывает другое, либо они не пересекаются, существует мероприятие, которое накрывает все остальные | |
| 5 | 15 | \(N \le 100\,000\) | В каждой паре мероприятий либо одно мероприятие накрывает другое, либо они не пересекаются | 1, 4 |
| 6 | 13 | \(N \le 500\) | У, 2–4 | |
| 7 | 13 | \(N \le 5\,000\) | У, 2–4, 6 | |
| 8 | 12 | \(N \le 100\,000\) | У, 1-7 | |
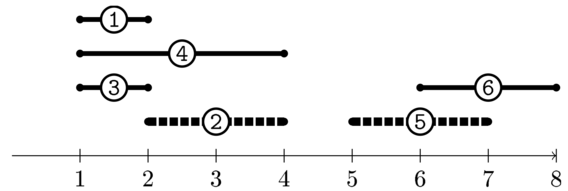
Рисунки визуализируют мероприятия. Мероприятие с началом в момент \(l_i\) и концом в момент \(r_i\) изображено в виде отрезка \([l_i, r_i]\).
 Исходное множество мероприятий в первом наборе входных данных в примере. Одно из возможных максимальных совместных множеств выделено жирным пунктиром.
Исходное множество мероприятий в первом наборе входных данных в примере. Одно из возможных максимальных совместных множеств выделено жирным пунктиром.
 Множество мероприятий, соответствующее ответу на первый набор входных данных в примере. Одно из возможных максимальных совместных множеств выделено жирным пунктиром.
Множество мероприятий, соответствующее ответу на первый набор входных данных в примере. Одно из возможных максимальных совместных множеств выделено жирным пунктиром.
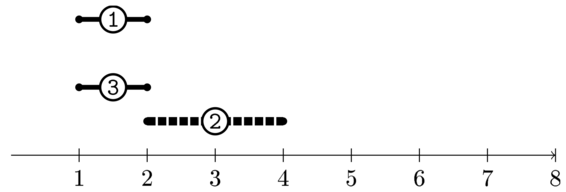
 Исходное множество мероприятий во втором наборе входных данных в примере. Одно из возможных максимальных совместных множеств выделено жирным пунктиром.
Исходное множество мероприятий во втором наборе входных данных в примере. Одно из возможных максимальных совместных множеств выделено жирным пунктиром.
 Множество мероприятий, соответствующее ответу на второй набор входных данных в примере. Одно из возможных максимальных совместных множеств выделено жирным пунктиром.
Множество мероприятий, соответствующее ответу на второй набор входных данных в примере. Одно из возможных максимальных совместных множеств выделено жирным пунктиром.
2 8 12 14 1 3 2 4 1 10 5 6 7 9 8 10 11 13 6 1 2 2 4 1 2 1 4 5 7 6 8
2 5 3 4 1 2 3