Всероссийская олимпиада школьников

Задача №115234. Интерактивные переходы

Кампус Иннополиса состоит из $n$ корпусов, соединённых $m$ переходами. Каждый переход соединяет два различных корпуса, никакие два корпуса не соединены более чем одним переходом.

Известно, что каждый корпус имеет подсветку, которая может быть включена или выключена. Изначально подсветка всех корпусов выключена. Диспетчер кампуса может за одно действие включить или выключить подсветку любого корпуса. Диспетчер может также нажимать кнопку включения подсветки, если она уже включена, или нажимать кнопку выключения, если она выключена. Данные действия не приводят к изменению состояния подсветки корпуса.

Аналогично, каждый переход имеет подсветку, которая может быть включена или выключена. Исходно подсветка всех переходов выключена. Однако в отличие от подсветки корпусов, подсветка переходов изменяется автоматически: если после очередного действия диспетчера состояние подсветки соединённых переходом корпусов оказывается одинаковым, то подсветка перехода также переходит в это состояние, а иначе она не меняется.

Другими словами, если после очередного действия диспетчера подсветка обоих корпусов, соединённых переходом, оказывается выключена, то подсветка перехода также выключается. Если подсветка обоих корпусов, соединённых переходом, оказывается включена, то подсветка перехода также включается. Если подсветка одного из корпусов оказывается включена, а другого — выключена, то состояние подсветки перехода не меняется.

Перед приездом участников олимпиады по информатике директор кампуса для каждого корпуса и каждого перехода определил, должен ли этот корпус или переход быть подсвечен.

Проверьте, может ли диспетчер выполнить пожелание директора, выполнив произвольное число действий. Если это возможно, то найдите любую такую последовательность действий. Решения, корректно определяющие возможность получить желаемое состояние подсветки, но не предъявляющие искомую последовательность действий, будут получать частичные баллы.

Входные данные

Каждый тест содержит один или несколько наборов входных данных. В первой строке теста задано целое число $t$ — количество наборов входных данных в тесте ($1 \le t \le 50\,000$). Далее следуют описания наборов. Каждый набор описывается следующим образом.

В первой строке заданы целые числа: $n$ — количество корпусов, и $m$ — количество переходов ($1 \le n \le 10^5$, $0 \le m \le 2\cdot 10^5$).

В следующих $m$ строках следуют описания переходов.

В $i$-й строке находятся целые числа $a_i$, $b_i$, $c_i$ — номера корпусов, соединённых $i$-м переходом, и требуемое состояние подсветки $i$-го перехода, соответственно ($1 \le a_i, b_i \le n$, $a_i \ne b_i$, $0 \le c_i \le 1$). Если $c_i=0$, то подсветка $i$-го перехода в результате должна быть выключена, а если $c_i = 1$, то включена.

В последней строке заданы $n$ целых чисел $d_1,d_2,\ldots,d_n$ — требуемое состояние подсветки корпусов ($0 \le d_i \le 1$). Если $d_v=0$, подсветка корпуса $v$ в итоге должна быть выключена, а если $d_v = 1$, то включена.

Сумма значений $n$ по всем наборам входных данных не превышает $10^5$. Сумма значений $m$ по всем наборам входных данных не превышает $2\cdot 10^5$.

Выходные данные

Для каждого набора входных данных:

Если не существует последовательности действий, получающей требуемое состояние подсветки корпусов и переходов, то выведите « NO ».
Если последовательность действий существует, то выведите « YES ». Если вы не хотите предъявлять саму последовательность действий, то выведите в следующей строке число $-1$ и перейдите к следующему набору входных данных. Если вы хотите предъявить последовательность действий, то выведите в следующей строке целое число $s$ — количество действий ($0 \le s \le 10^6$, сумма значений $s$ по всем наборам входных данных не должна превышать $10^6$), а в следующих $s$ строках выведите сами действия.

В $i$-й строке ($1 \le i \le s$) выведите два целых числа: $v_i$ — номер корпуса, в котором изменяется состояние подсветки, и $x_i$ — новое состояние подсветки ($1 \le v_i \le n$, $0 \le x_i \le 1$, если $x_i=0$, то подсветка корпуса $v_i$ выключается, если $x_i=1$, то подсветка корпуса $v_i$ включается).

Система оценки

Обозначим за $N$ сумму значений $n$ во всех наборах входных данных в одном тесте, за $M$ — сумму значений $m$ во всех наборах тестовых данных в одном тесте.

Если решение выводит неправильную последовательность действий на одном из тестов подзадачи, то оно получает $0$ баллов за подзадачу. Если на хотя бы одном тесте подзадачи решение выводит $-1$ и на каждом тесте подзадачи выводит либо верную последовательность действий, либо $-1$, то оно получает половину баллов за подзадачу. Если на каждом тесте подзадачи решение выводит верную последовательность действий, то оно получает полный балл за подзадачу.

		Ограничения
Подз.	Баллы	$N, n$	$M, m$	Дополнительные ограничения	Необх. подзадачи
1	4	$n \le 3$	—	$t \le 230$
2	10	$N \le 2000$	$M \le 2000$	$n+m \le 14$
3	8	—	—	$c_i=1$
4	6	—	—	$m=n-1$, $a_i=1$, $b_i=i+1$
5	6	—	—	$d_{a_i}=c_i$, $a_i \lt b_i$
6	8	$N \le 2000$	—	$m=n-1$, $a_i=i$, $b_i=i+1$
7	8	—	—	$m=n-1$, $a_i=i$, $b_i=i+1$	6
8	10	$N \le 2000$	—	$m=n-1$, из любого корпуса можно добраться до любого другого по переходам	6
9	6	—	—	$m=n-1$, из любого корпуса можно добраться до любого другого по переходам	4, 6–8
10	6	—	—	$m=n$, $a_i=i$, $b_i=i \% n+1$
11	10	$N \le 2000$	$M \le 2000$	—	2, 6, 8
12	18	—	—	—	1–11

Примечание

В примере из условия пять тестовых наборов данных.

В первом наборе даны 4 корпуса, обозначенных кружками, и 4 перехода, обозначенных линиями. Наличие подсветки корпуса или перехода обозначено жирной линией. Получить нужную подсветку можно за 5 действий. На рисунках ниже изображены начальное состояние подсветки и состояние после каждого действия.

$\text{[math]}$

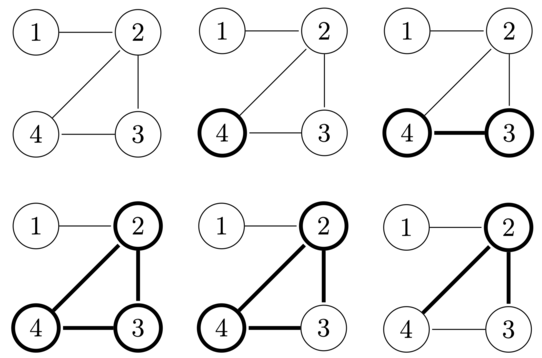
Во втором наборе нужно получить следующую конфигурацию из 4 корпусов и 4 переходов, но сделать это невозможно.

$\text{[math]}$

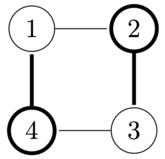
В третьем наборе один корпус, в котором нужно включить подсветку. Это можно сделать за одно действие.

В четвёртом примере один корпус, в котором подсветка должна быть выключена. Возможной последовательностью действий является единственное действие выключения подсветки в корпусе. Это является корректной действием, несмотря на то, что подсветка уже была выключена.

В пятом примере два корпуса и один переход, подсветка везде должна быть выключена. Пустая последовательность действий является корректной последовательностью, приводящей к такой конфигурации.

Примеры

Входные данные

Выходные данные

Сдать: для сдачи задач необходимо войти в систему