Задача №115239. Экзамен в ГИББД
Миша — начинающий автомобилист. После успешного прохождения теоретической части экзамена на права ему оставалось немногое — сдать вождение в ГИББД. Но, как оказалось, не все так просто, ведь Миша не умеет управлять автомобилем на льду.
Трасса, на которой проходит экзамен в ГИББД, находится в поле и представляет собой \(n\) перекрестков, для \(i\) от \(1\) до \(n - 1\) между \(i\)-м и \((i+1)\)-м перекрестком есть дорога длины \(d_i\). Изначально на \(i\)-м перекрестке содержится \(w_i\) единиц льда.
Для проведения экзамена инспекторы выбирают непрерывный подотрезок \([l, r]\) трассы: все перекрестки с номерами от \(l\) до \(r\) включительно и все дороги между ними. Трасса для экзамена должна быть циклической, поэтому инспекторы после выбора \(l\) и \(r\) также соединяют перекрестки с номерами \(l\) и \(r\) временной дорогой длины \(x\).
Инспекторы не хотят, чтобы Миша сдал экзамен, поэтому все дороги трассы экзамена должны быть покрыты льдом. Для этого необходимо переместить на дорогу лед с перекрестков, которые она соединяет, одна единица льда может покрыть одну единицу дороги. Следовательно, суммарное количество льда, перемещенное на дорогу, должно быть не меньше, чем ее длина. Разумеется, на две соседние дороги с каждого перекрестка можно суммарно переместить не больше льда, чем там находится.
К сожалению, текущего количества льда может не хватить, чтобы покрыть все дороги, поэтому инспекторы интересуются, какое минимальное суммарное количество льда нужно добавить на перекрестки, чтобы было возможно покрыть все дороги и не дать Мише сдать экзамен.
Вам предстоит обработать три вида запросов: изменить количество льда на каком-то перекрестке, изменить длину какой-то дороги и решить задачу для подотрезка трассы.
Первая строка содержит два целых числа \(n\) и \(q\) — количество перекрестков и запросов, соответственно (\(2 \le n \le 2 \cdot 10^5, 1 \le q \le 2 \cdot 10^5\)).
Вторая строка содержит \(n\) целых чисел \(w_i\) — изначальное количество льда на каждом перекрестке (\(1 \le w_i \le 10^9\)).
Третья строка содержит \(n - 1\) целых чисел \(d_i\) — изначальная длина каждой дороги между соседними перекрестками (\(1 \le d_i \le 10^9\)).
В следующих \(q\) строках описаны запросы:
- \(1\) \(p\) \(x\) \((1 \le p \le n, 1 \le x \le 10^9)\) — выполнить присваивание \(w_p := x\);
- \(2\) \(p\) \(x\) \((1 \le p \le n - 1, 1 \le x \le 10^9)\) — выполнить присваивание \(d_p := x\);
- \(3\) \(l\) \(r\) \(x\) \((1 \le l < r \le n\), \(1 \le x \le 10^9)\) — узнать минимальное количества льда, которое надо добавить на перекрестки, для трассы, образованной подотрезком перекрестков от \(l\) до \(r\) включительно, а также дорогой длины \(x\), замыкающей цикл. Обратите внимание, что третий запрос не изменяет количество льда на перекрестках, вам нужно лишь ответить, какое количество льда необходимо добавить на перекрестки, чтобы было возможно покрыть все дороги льдом. После каждого запроса инспекторы демонтируют временную дорогу, поэтому в других запросах ее учитывать не надо.
Гарантируется, что есть хотя бы один запрос третьего типа.
Для каждого запроса третьего типа выведите минимальное суммарное количество льда, которое нужно добавить на перекрестки, чтобы было возможно покрыть всю циклическую трассу льдом.
На рисунке приведены иллюстрации к примеру. Пунктирными линиями обозначены временные дороги, замыкающие цикл. На перекрестках обозначено текущее и добавленное количество льда, на дорогах обозначено количество льда, перемещенное с перекрестков.
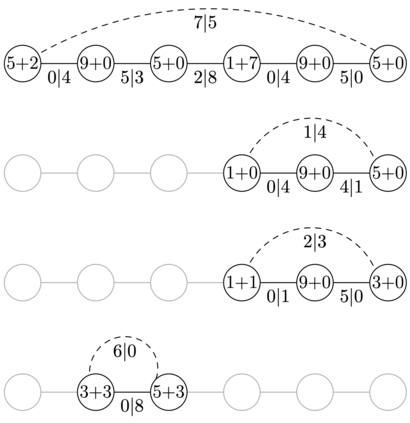
6 7 5 9 5 1 9 5 4 8 10 4 5 3 1 6 12 3 4 6 5 2 4 1 1 6 3 3 4 6 5 1 2 3 3 2 3 6
9 0 1 6