ВКОШП: ВКОШП 2023

Совсем скоро Новый Год! В честь этого Матвей решил купить себе новогоднюю ёлку. Он пошёл в магазин, где продаются графы-ёлки. Но, когда он пришёл, не смог определиться, так как выбор был огромный. Тогда он решил посчитать, сколько существует ёлок высоты \(n\).

Матвей считает дерево с корнем в вершине 1 ёлкой высоты \(n\) , если оно удовлетворяет следующим условиям:

• будем считать, что корень находится на первом слое, его дети — на втором слое и так далее, дети вершины \(i\)-го слоя находятся на \((i+1)\)-м слое. Тогда на \(i\)-м слое должно находиться ровно \(i\) вершин;

• у каждой вершины не более двух детей;

• пронумеруем вершины по слоям сверху вниз целыми числами, начиная с 1. На одном слое пронумеруем вершины слева направо. После этого рассмотрим две вершины \(u\), \(v\), такие, что они находятся на одном слое и \(u < v\), тогда все дети вершины \(u\), если они есть, должны иметь меньший номер, чем дети вершины \(v\).

Матвей считает ёлки различными, если существуют числа \(i\), \(j\), такие, что в одной ёлке есть ребро между вершинами \(i\) и \(j\), а в другой такое ребро отсутствует.

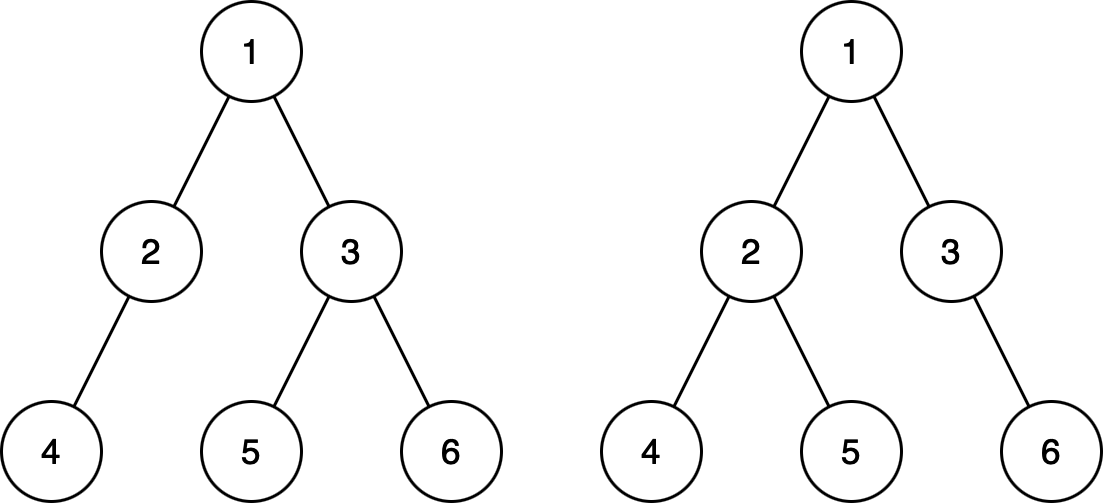
Для высоты \(3\) есть две различные ёлки, они приведены на рисунке.

Вам нужно посчитать количество различных ёлок высоты \(n\).