Всероссийская командная олимпиада

Задача №115246. Улицы Флатландии

Флатландия — страна, расположенная на плоскости. Всего во Флатландии $n$ городов, соединенных $n - 1$ двухсторонними дорогами так, что от любого города можно добраться до любого другого. Город номер $i$ располагается в точке с координатами $(x_i, y_i)$.

Недавно во Флатландии решили провести дорожную реформу и назначить каждой дороге название. Однако для экономии ресурсов было постановлено использовать как можно меньше различных названий. Нескольким дорогам можно назначить одно и то же название, если все эти дороги образуют простой путь и для любых двух последовательных дорог $(u, v)$ и $(v, w)$ на этом пути пара направленных дорог $u \to v$ и $v \to w$ совместима и пара направленных дорог $w \to v$ и $v \to u$ совместима .

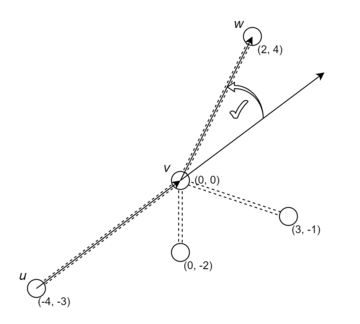
В данном случае пару дорог $u \to v$ и $v \to w$ будем называть совместимой, если при повороте вектора $\overrightarrow{uv}$, отложенного из точки $v$, к вектору $\overrightarrow{vw}$ относительно точки $v$ не встречается никакая другая дорога, выходящая из города $v$.

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
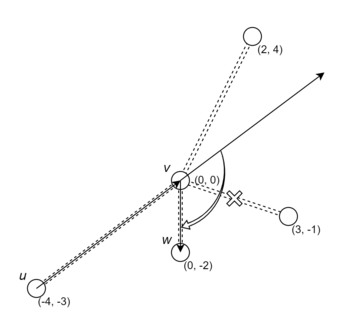
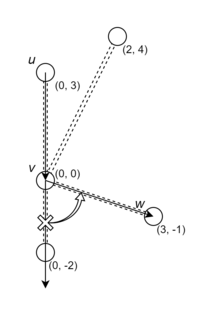
Совместимая пара $u \to v$ и $v \to w$	Несовместимая пара $u \to v$ и $v \to w$	Сонаправленная дорога

Обратите внимание, что дороги должны быть совместимы в обе стороны, тогда как иллюстация показывает совместимость только в одном направлении. Также, если вектор $\overrightarrow{uv}$, отложенный из $v$, оказывается сонаправлен с некоторой дорогой, она считается единственной совместимой с дорогой $(u, v)$.

Путь из одной или более дорог с одинаковым названием называется магистралью . Определите минимальное число магистралей с различными названиями, на которые можно разбить все дороги Флатландии.

Входные данные

В первой строке ввода дано единственное целое число $n$ — количество городов во Флатландии ($1 \le n \le 2 \cdot 10^5$).

В $i$-й из следующих $n$ строк даны два целых числа $x_i$ и $y_i$ — координаты $i$-го города ($|x_i|, |y_i| \le 10^9$). Гарантируется, что никакие два города не расположены в одной точке плоскости.

Следующие $n - 1$ строк описывают дороги во Флатландии — $i$-я строка содержит номера городов $u_i$ и $v_i$, соединяемых $i$-й дорогой ($1 \le u_i, v_i \le n$). Гарантируется, что между любыми двумя городами существует ровно один путь.

Также гарантируется, что никакие две дороги, исходящие из одного города, не сонаправлены. Но не гарантируется , что отрезки на плоскости, соответствующие дорогам, не пересекаются.

Выходные данные

Выведите единственное целое число — минимальное количество магистралей после именования всех дорог Флатландии.

Примечание

В условии приведены иллюстрации к двум примерам. В первом примере можно совместить в магистраль пути $(2, 1, 4)$ и $(3, 1, 5)$. Во втором примере получить меньше трех магистралей не получится, потому что дороги $(1, 5)$ и $(1, 4)$ совместимы только друг с другом, а $(1, 2)$ и $(1, 3)$ — не совместимы.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

Сдать: для сдачи задач необходимо войти в систему