Задача №115279. Защита крепости
Флатландцы строят крепость на клетчатой плоскости. Крепость будет иметь несколько контуров обороны, каждый из которых будет представлять собой прямоугольник со сторонами, проходящими по границам клеток.
Первый, внешний, контур обороны должен иметь форму прямоугольника размера \(h \times w\), а каждый следующий контур должен находиться строго внутри всех предыдущих. Контуры обороны не должны иметь общих точек.
Уровнем защиты клетки назовем количество контуров обороны, внутри которых она лежит. Уровень защиты крепости равен сумме уровней защиты всех входящих в нее клеток. Например, уровень защиты крепости на рисунке равен \(16 \cdot 1 + 8\cdot 2 + 3 = 35\).
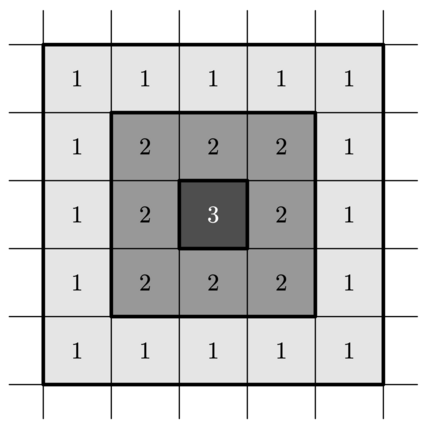
Флатландцы заинтересовались всеми возможными способами построить крепость. Для каждого способа они считают уровень защиты этой крепости, а затем вычисляют сумму этих значений по всем способам. Помогите им посчитать эту сумму. Ответ может быть довольно большим, выведите его остаток от деления на \(10^9 + 7\).
На первой строке ввода находятся два целых числа \(h\) и \(w\) (\(1 \le h, w \le 400\)).
Выведите одно число: сумму уровней защиты для всех способов построить крепость, взятую по модулю \(10^9 + 7\).
Все способы построить крепость в первом примере приведены на рисунке.

Все способы построить крепость во втором примере приведены на рисунке.
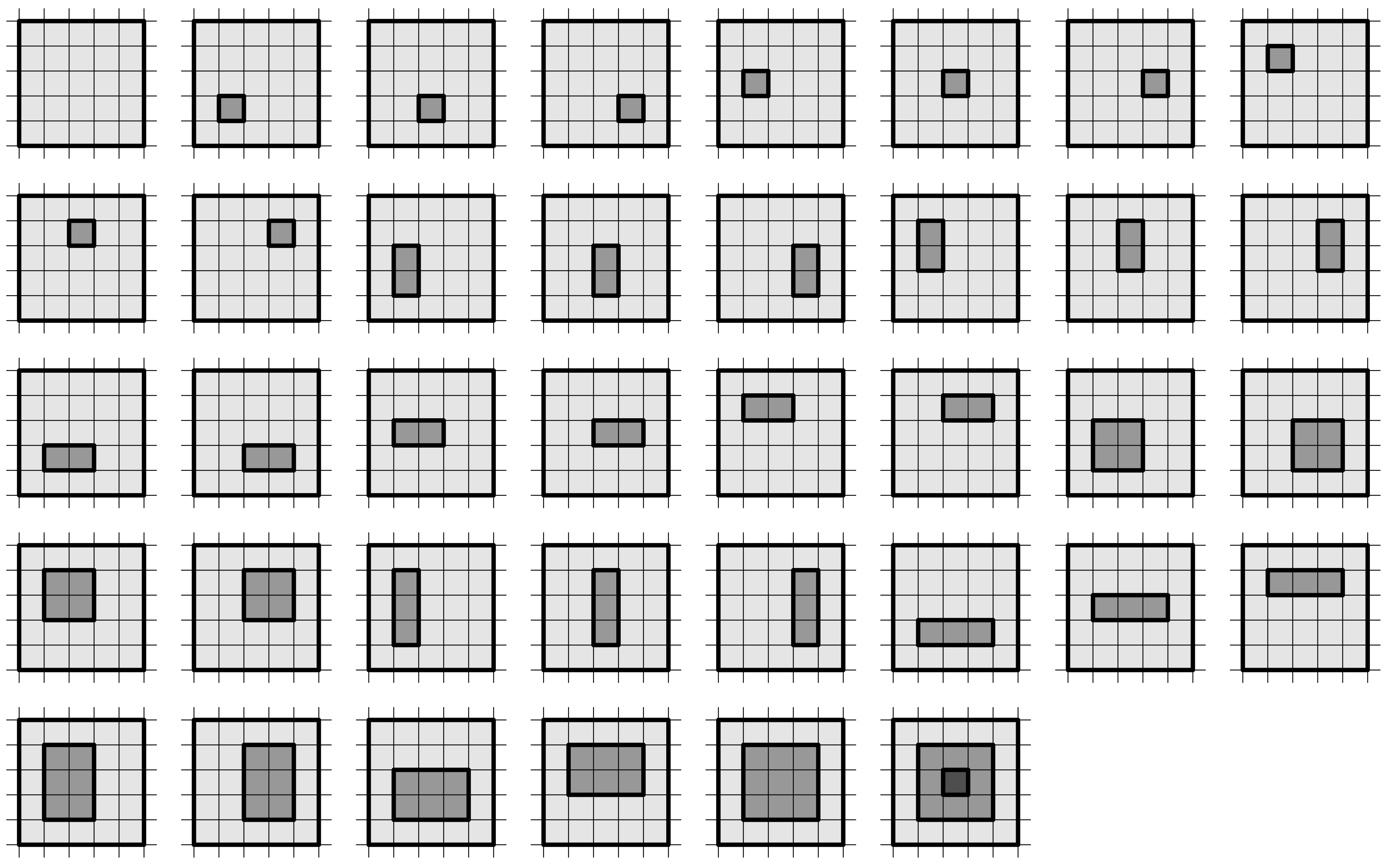
3 3
19
5 5
1060