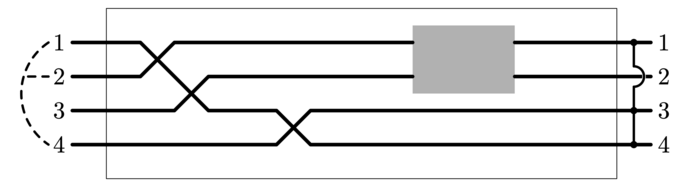
Задача №115280. Головоломка с проводами
Это интерактивная задача. В процессе решения ваша программа должна взаимодействовать с программой жюри, используя стандартные потоки ввода и вывода.
Друзья играют в игру-головоломку, которая устроена следующим образом. Есть \(n\) одинаковых проводов, проложенных через непрозрачную трубу. Будем называть один из концов трубы левым, а другой — правым. С каждого из концов трубы игроки видят \(n\) проводов, которые помечены различными числами от \(1\) до \(n\), при этом один и тот же провод с разных сторон может быть помечен разными номерами.
Цель игры — установить соответствие между концами проводов, то есть для каждого \(i\) от \(1\) до \(n\) определить, каким числом \(a_i\) помечен на левом конце трубы провод, помеченный числом \(i\) на правом конце трубы.
Для этого можно выполнять следующие запросы. Выберем число \(k\) (\(1 \le k \le n\)). После этого разобъём провода у правого конца трубы на \(k\) непустых групп и соединим все провода внутри одной группы. Затем с помощью специального устройства можно проверить для каждой пары проводов у их левого конца, соединены ли их правые концы. Таким образом, для левых концов проводов известно, помеченные какими числами слева провода попали в одну группу.
Требуется установить соответствие между левыми и правыми концами проводов, выполнив ровно три описанных запроса.
Для лучшего понимания действий, которые выполняются в задаче, настоятельно рекомендуем ознакомиться с примером, описанным ниже.
Сначала ваша программа должна считать со стандартного потока ввода число \(n\) (\(3 \le n \le 200\)). Затем она должна выполнить три запроса.
Чтобы выполнить запрос, необходимо сначала вывести в стандартный поток вывода на отдельной строке число \(k\) — количество групп, а затем \(n\) целых чисел \(g_1, g_2, \ldots, g_n\). Каждое число должно быть в диапазоне от \(1\) до \(k\), каждое число от \(1\) до \(k\) должно встречаться хотя бы один раз. число \(g_i\) задает номер группы, в которую определяется правый конец провода, помеченный числом \(i\). Все правые концы проводов, попавшие в одну группу, соединяются.
В ответ на это программа жюри сообщит вашей программе, какие левые концы проводов соответствуют проводам, правые концы которых попали в одну группу. А именно, она выведет информацию о \(k\) группах. Информация о \(j\)-й группе начинается с числа \(s_j\) на отдельной строке, это число задает количество проводов в этой группе, а затем следует \(s_j\) чисел — номера, которыми помечены левые концы проводов, попавшие в эту группу. При этом порядок, в котором программа жюри перечисляет группы, может быть произвольным. В частности, он может отличаться от порядка, в котором группы были пронумерованы в запросе. Номера концов проводов в каждой группе также могут быть перечислены в произвольном порядке.
Выполнив три описанных запроса, ваша программа должна вывести \(n\) чисел \(a_1, a_2, \ldots, a_n\), где \(a_i\) — номер, которым помечен левые конец провода, правый конец которого помечен как \(i\).
В приведенном примере события развиваются следующим образом.
В трубе находятся 4 провода.

В первом запросе программа участника сделала три группы проводов, соединив провода с номерами правых концов 1 и 2, провод с номером правого конца 3 не соединен с другими, провод с номером правого конца 4 также не соединен с другими.
Программа жюри сообщает, что провода с номерами левого конца 2 и 3 в одной группе, провод с номером левого конца 1 в отдельной группе, провод с номером левого конца 4 также в отдельной группе.

На основании этого программа участника понимает, что провода с номерами левых концов 2 и 3 соответствуют в некотором порядке проводам с номерами правых концов 1 и 2, а провода с номерами левых концов 1 и 4 — проводам с номерами правых концов 3 и 4.
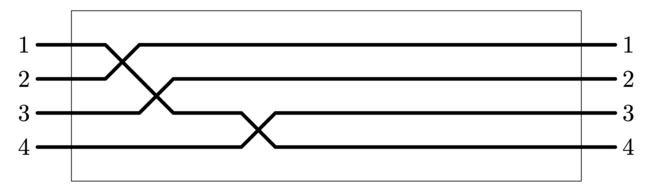
Вторым запросом программа участника создала две группы проводов и соединила правые концы проводов с номерами правых концов 1, 2 и 3, провод с номером правого конца 4 не соединен с другими.
Программа жюри сообщает, что объединены в группу оказались провода с номерами левых концов 2, 3 и 4.
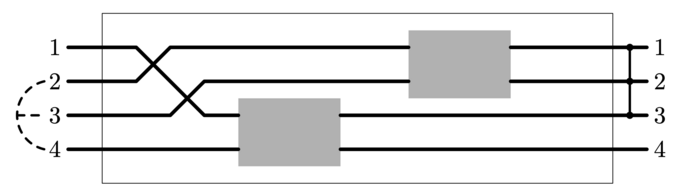
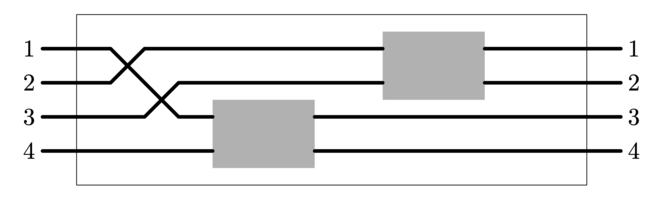
Это позволило программе участника понять, что провод с правым концом 4 на левом конце помечен числом 1, а следовательно провод с правым концом 3 на левом конце помечен числом числом 4.
Третий запрос аналогично позволяет различить провода с правым концом 1 и 2, таким образом соответствие левых и правых концов полностью установлено.