Задача №115364. Хорошее начало
Вам предстоит помочь строительной бригаде при укладке кровли на нескольких крышах. Для каждой из них вам необходимо определить, можно ли полностью покрыть крышу одинаковыми листами кровли.
Каждая крыша представляет собой прямоугольник размером \(w \times h\), расположенный на плоскости с левым нижним углом в точке \((0, 0)\). Для укладки используются прямоугольные листы кровли размером \(a \times b\). При этом:
-
Листы нельзя поворачивать (даже на \(90^\circ\)).
-
Листы не должны пересекаться между собой (но могут соприкасаться сторонами).
- Листы могут выходить за пределы прямоугольника крыши.
На каждой крыше уже размещены два таких листа. Известно, что листы не пересекаются между собой и что каждый из них хотя бы частично покрывает крышу.
Вам необходимо для каждой крыши сказать, можно ли покрыть всю крышу, соблюдая все условия.
В первой строке дано целое число \(n\) (\(1 \le n \le 10^4\)) — число крыш, для которых вам нужно решить задачу.
Далее в следующих \(2n\) строках для каждой крыши идет ее описание в следующем формате:
-
В первой строке описания крыши даны четыре целых числа \(w, h, a, b\) (\(1 \le w, h, a, b \le 10^9\)) — размеры крыши и размеры листов кровли, соответственно.
- Во второй строке описания крыши даны четыре целых числа \(x_1\), \(y_1\), \(x_2\) и \(y_2\) (\(-a + 1 \le x_1, x_2 \le w - 1, -b + 1 \le y_1, y_2 \le h - 1\)) — координаты левых нижних углов уже положенных листов кровли. Гарантируется, что данные листы кровли не пересекаются.
Для каждой крыши выведите Yes , если крышу возможно дозамостить, соблюдая все условия. Если замостить крышу, выполнив все требования, невозможно, выведите No .
В данной задаче \(10\) тестов, помимо тестов из условия, каждый из них оценивается в \(10\) баллов.
Гарантируется, что решения, корректно работающие при \(a \le 2, b \le 2\), наберут не менее \(50\) баллов.
В примере первую крышу можно дозамостить, например, следующим образом:

В примере вторую крышу полностью замостить невозможно:
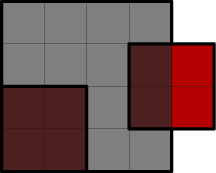
3 6 5 2 3 -1 -2 5 4 4 4 2 2 0 0 3 1 2 2 1 1 0 0 1 1
Yes No Yes