Задача №115392. Простая задача для любителей
На бесконечной плоскости заданы \(n\) секторов, каждый сектор представляет собой направленный угол \(AOB\), где \(O\) — начало координат, направление угла считается против часовой стрелки от луча \(OA\) к лучу \(OB\). Величина угла не превосходит \(180^{\circ}\).
Даны \(q\) точек на плоскости. Каждая точка имеет свой вес \(w_i\).
Для каждого сектора необходимо найти суммарный вес точек, принадлежащих данному сектору. Точка принадлежит сектору, если она находится внутри или на его границе. Обратите внимание, что одна точка может принадлежать нескольким секторам.
Первая строка содержит одно целое число \(n\) (\(1 \le n \le 2 \cdot 10^5\)) — количество секторов. В следующих \(n\) строках описаны секторы.
Каждый сектор задается четырьмя целыми числами \(x_{A}\), \(y_{A}\), \(x_{B}\) и \(y_{B}\) (\(0 \leq |x_{A}|, |y_{A}|, |x_{B}|, |y_{B}| \leq 10^{9}\)) — координаты точек \(A\) и \(B\). Гарантируется, что точки \(A\) и \(B\) не совпадают с началом координат, и величина направленного угла лежит в диапазоне \((0^{\circ}; 180^{\circ}]\).
Следующая строка содержит одно целое число \(q\) (\(1 \le q \le 2 \cdot 10^5\)) — количество точек. В следующих \(q\) строках описаны точки.
Каждая точка задается тремя целыми числами \(x\), \(y\) и \(w\) (\(0 \leq |x|, |y| \leq 10^{9}\), \(0 \leq w \leq 10^{9}\)) — координаты и вес. Гарантируется, что точка \((x, y)\) не совпадает с началом координат.
Выведите \(n\) целых чисел \(s_{1}, s_{2}, \ldots, s_{n}\), где \(s_{i}\) — суммарный вес точек, принадлежащих \(i\)-му сектору.
На рисунке изображен пример из условия. Рядом с каждой точкой подписан её вес.
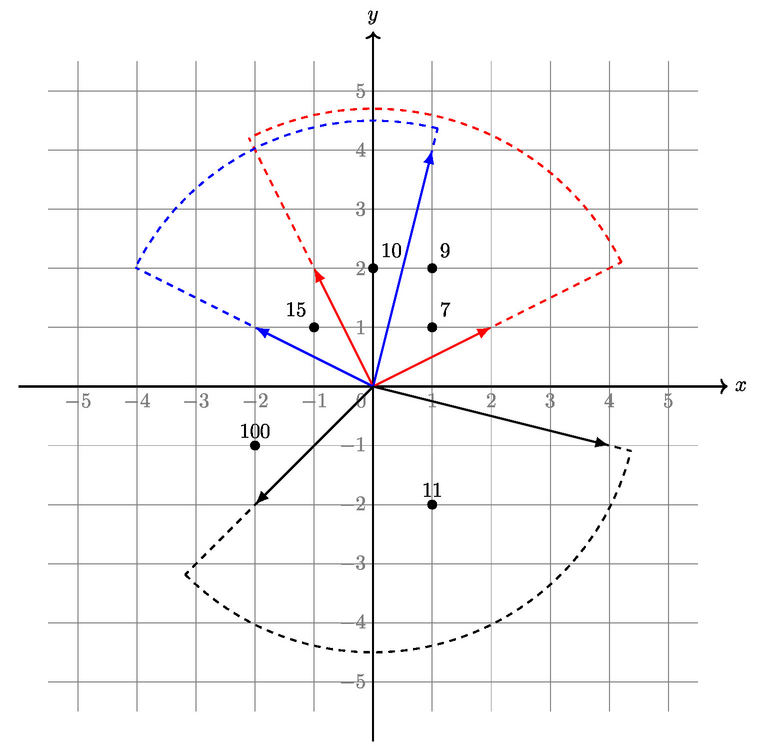
3 2 1 -1 2 1 4 -2 1 -2 -2 4 -1 6 0 2 10 1 2 9 -1 1 15 1 1 7 -2 -1 100 1 -2 11
26 25 11