Задача №115402. Минимизация инверсий
Дана таблица \(a\), состоящая из \(r\) строк и \(c\) столбцов, в которой записаны в произвольном порядке все различные числа от \(1\) до \(r \cdot c\). Элементы этой таблицы переносятся в изначально пустой массив \(b\).
Пока таблица непустая, над ней выполняется одно из двух действий:
-
Дописать в конец массива элементы первой строки таблицы в порядке от элемента в первом столбце до элемента в последнем и удалить первую строку из таблицы.
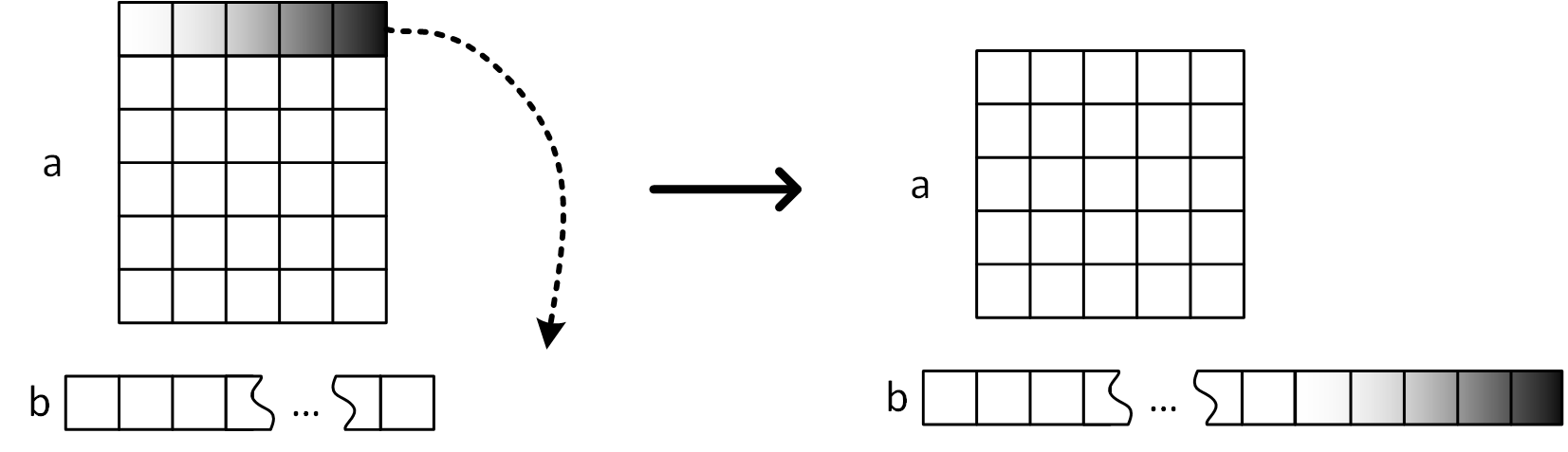
-
Дописать в конец массива элементы первого столбца таблицы в порядке от элемента в первой строке до элемента в последней и удалить первый столбец из таблицы.
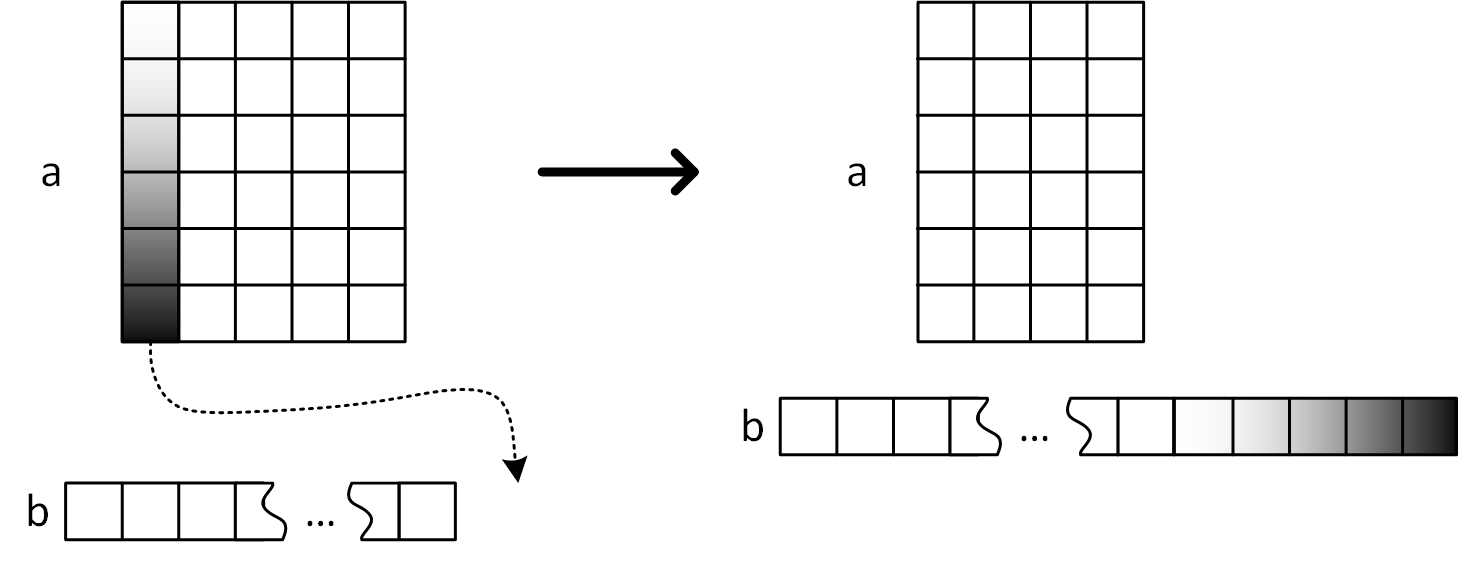
Порядок действий требуется выбирать таким, чтобы количество инверсий в полученном массиве после применения всех операций было минимальным.
Инверсией называется такая пара индексов элементов массива \(1 \le i < j \le r\cdot c\), что \(b_i > b_j\).
Первая строка содержит два целых числа \(r\) и \(c\) (\(r \le c\), \(1 \le r \cdot c \le 2\,000\,000\)) — количество строк и столбцов в таблице соответственно.
В следующих \(r\) строках содержится описание таблицы \(a\). В \(i\)-й из них содержится \(c\) целых чисел \(a_{i1}\), \(\ldots\), \(a_{ic}\) (\(1 \le a_{ij} \le r \cdot c\)) — элементы матрицы \(a\).
Гарантируется, что все числа в таблице \(a\) различны.
Выведите одно число — минимально возможное количество инверсий в массиве \(b\) после применения всех операций.
| Ограничения | |||||
| Подзадача | Баллы | \(r\) | \(c\) | \(r \cdot c\) | Необходимые подзадачи |
| 1 | 15 | \(r + c \le 14\) | У | ||
| 2 | 18 | – | \( r \cdot c \le 500 \) | У, 1 | |
| 3 | 5 | Все строки и столбцы отсортированы в возрастающем порядке и \( r \cdot c \le 250\,000 \) | – | ||
| 4 | 7 | \(r = 1\) | – | \( r \cdot c \le 250\,000 \) | – |
| 5 | 6 | \(r \le 2\) | 4 | ||
| 6 | 2 | \(r \le 20 \) | У, 1, 4, 5 | ||
| 7 | 10 | \(r,\ c \le 100\) | – | У, 1 | |
| 8 | 2 | – | \(r \cdot c \le 10\,000\) | У, 1, 2, 7 | |
| 9 | 1 | \(r \le 100\) | \(c \le 1000\) | – | У, 1, 2, 7 |
| 10 | 1 | \(c \le 2500\) | У, 1, 2, 7, 9 | ||
| 11 | 1 | \(c \le 5000\) | У, 1, 2, 7, 9, 10 | ||
| 12 | 1 | \(c \le 7500\) | У, 1, 2, 7, 9–11 | ||
| 13 | 1 | \(c \le 10\,000\) | У, 1, 2, 7–12 | ||
| 14 | 4 | \(c \le 15\,000\) | У, 1, 2, 7–13 | ||
| 15 | 2 | \(c \le 20\,000\) | У, 1, 2, 7–14 | ||
| 16 | 3 | \(r,\ c \le 200\) | У, 1, 7 | ||
| 17 | 3 | \(r,\ c \le 400\) | У, 1, 7, 16 | ||
| 18 | 4 | \(r,\ c \le 600\) | У, 1, 2, 7, 16, 17 | ||
| 19 | 1 | \(r,\ c \le 800\) | У, 1, 2, 7, 16–18 | ||
| 20 | 1 | \(r,\ c \le 1000\) | У, 1, 2, 7, 9, 16–19 | ||
| 21 | 1 | \(r,\ c \le 1200\) | У, 1, 2, 7, 9, 16–20 | ||
| 22 | 1 | \(r,\ c \le 1400\) | У, 1, 2, 7, 9, 16–21 | ||
| 23 | 1 | – | \(r \cdot c \le 100\,000\) | У, 1, 2, 7–9, 16 | |
| 24 | 1 | \(r \cdot c \le 250\,000\) | У, 1–10, 16, 17, 23 | ||
| 25 | 4 | \(r \cdot c \le 500\,000\) | У, 1–11, 16–18, 23, 24 | ||
| 26 | 1 | \(r \cdot c \le 750\,000\) | У, 1–12, 16–19, 23–25 | ||
| 27 | 1 | \(r \cdot c \le 1\,000\,000\) | У, 1–13, 16–20, 23–26 | ||
| 28 | 1 | \(r \cdot c \le 1\,500\,000\) | У, 1–14, 16–21, 23–27 | ||
| 29 | 1 | – | У, 1–28 | ||
В первом примере минимальное число инверсий достигается при двукратном удалении первой строки. В результате массив \(b\) будет равен \([3, 4, 1, 5, 6, 2]\). Такой массив содержит \(6\) инверсий.
Во втором примере для достижения минимального числа инверсий можно сначала удалить первый столбец, а потом два раза удалить первую строку. В результате массив \(b\) будет равен \([2, 1, 3, 4, 6, 5]\). Такой массив содержит \(2\) инверсии.
2 3 3 4 1 5 6 2
6
2 3 2 3 4 1 6 5
2