Открытая олимпиада школьников по программированию

Задача №115406. Мечтать не вредно

В свадебном агентстве М. намечаются массовые увольнения. Все сотрудники вместо работы заняты подсчётом дней, через которые, при удачном стечении обстоятельств, смогут возглавить компанию.

Структура компании представляет собой подвешенное дерево с корнем в вершине номер $1$. Непосредственным начальником сотрудника с номером $v$ является сотрудник с номером $p_v$. Уровень компетенции сотрудника $v$ задаётся параметром $s_v$. Этот параметр различен для всех сотрудников. Чем выше уровень компетенции, тем полезнее сотрудник для компании. Обратите внимание, что в результате непрозрачного процесса найма могло оказаться, что менее компетентный сотрудник является начальником более компетентного.

В результате больших кадровых перестроений каждый день будет увольняться генеральный директор, который находится в корне рабочей иерархии. Если в компании остаются сотрудники, его место займёт наиболее компетентный непосредственный подчинённый. После этого остальные подчинённые бывшего директора станут подчинёнными нового директора. Посмотрите пояснения к примерам для лучшего понимания условия.

Каждый из сотрудников легко посчитал, через какое количество дней он сможет стать генеральным директором. Многие оказались не готовы так долго ждать, ведь побыть директором удастся только один день! Чтобы ускорить этот процесс, они готовы «отменить» одного из коллег. У «отменённого» сотрудника уровень компетенции падает до $0$, так как никто больше не готов с ним взаимодействовать.

Вам предстоит ответить на $q$ запросов. В $k$-м запросе сотрудник с номером $v_k$ интересуется наименьшим количеством дней, через которое он сможет возглавить компанию, если он готов «отменить» ровно одного сотрудника. Все запросы воображаемые и независимые, а реальные уровни компетенции сотрудников остаются неизменными для всех запросов.

Входные данные

Первая строка содержит два целых числа $n$, $q$ ($2 \le n \le 300\,000$, $1 \le q \le n$) — число сотрудников и количество запросов.

Вторая строка содержит $n - 1$ целое число $p_2$, $p_3$, $\ldots$, $p_{n}$ ($1 \le p_i < i$) — непосредственные начальники сотрудников с номерами от $2$ до $n$.

Третья строка содержит $n$ целых чисел $s_1$, $s_2$, $\ldots$, $s_n$ ($1 \le s_i \le n$) — уровни компетенции сотрудников. Гарантируется, что они различны.

Четвёртая строка содержит $q$ целых чисел $v_1$, $v_2$, $\dots$, $v_q$ ($1 \le v_i \le n$) — запросы на повышение. Гарантируется, что все числа $v_i$ различны.

Выходные данные

Выведите $q$ целых чисел через пробел — минимальное количество дней, через которое сотрудники $v_1, v_2, \dots, v_q$ могут стать директорами.

Примечание

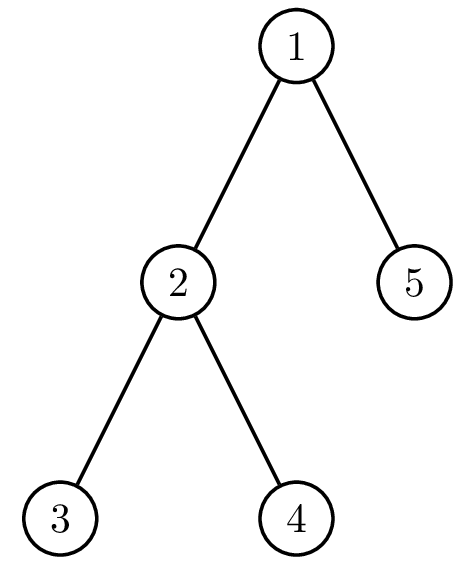
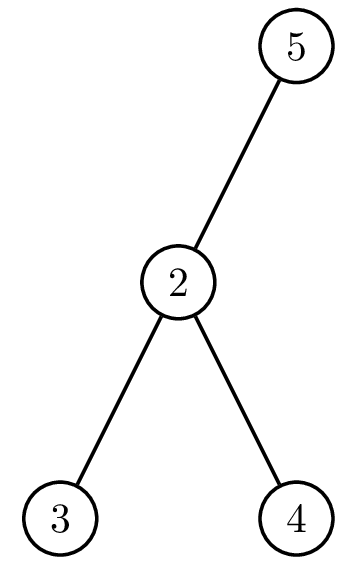
В тестовом примере пятый сотрудник может возглавить компанию за 1 день. Для этого достаточно «отменить» второго сотрудника. Структура компании в этом случае будет меняться следующим образом:

$\text{[math]}$	$\text{[math]}$
Начальная структура	День 1

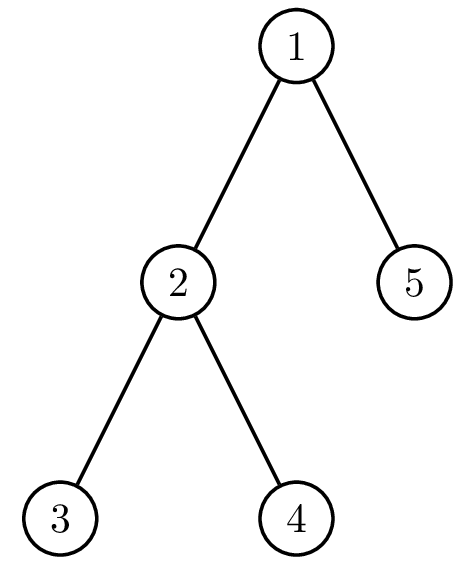
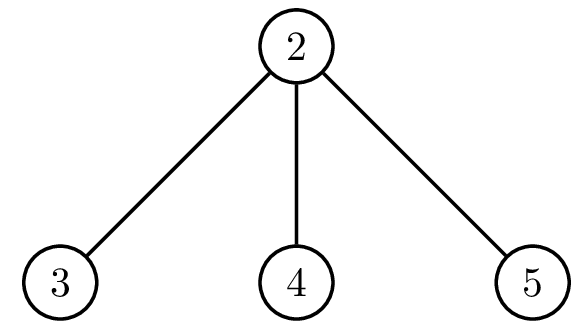
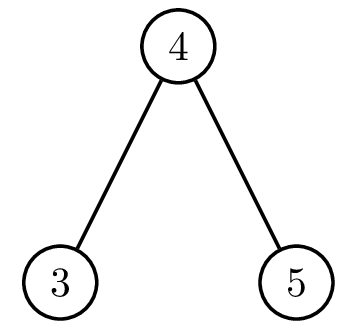
Третий сотрудник может возглавить компанию за 3 дня. Для этого достаточно «отменить» пятого или четвёртого сотрудника. Если отменить пятого, то структура компании будет меняться следующим образом:

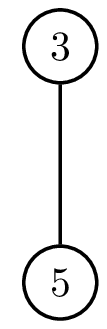
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
Начальная структура	День 1	День 2	День 3

Первый сотрудник уже является главой компании, поэтому на соответствующий запрос ответ $0$.

Четвёртый сотрудник может стать главой компании за два дня. Достаточно, аналогично примеру выше, «отменить» пятого сотрудника.

Система оценки

Тесты к этой задаче состоят из девяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, что прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.

		Доп. ограничения
Группа	Баллы	n	q	Необх. группы	Комментарий
0	0	–	–	–	Тесты из условия
1	10	–	–	–	$p_i = 1$ или $p_i = i - 1$, причем $p_i = 1$ для не более двух номеров $i$
2	6	–	–	1	$p_i = 1$ или $p_i = i - 1$
3	8	$n \le 50$	$q \le 50$	0
4	13	$n \le 1000$	$q \le 1000$	0, 3
5	11	–	$q \le 100$	0, 3
6	9	–	–	–	$p_i = \lfloor \frac{i}{2} \rfloor $
7	11	–	–	0, 3, 6	Количество начальников* у любого сотрудника не превосходит $100$
8	14	–	–	–	$s_i \gt s_{p_i}$ для любого $i \gt 1$
9	18	–	–	0 – 8	Oﬄine-проверка.

Начальники* сотрудника — это множество из его непосредственного начальника и всех начальников его непосредственного начальника.

Примеры

Входные данные

Выходные данные

1 3 0 2

Сдать: для сдачи задач необходимо войти в систему