Задача №115430. Двухэтажный адвент-календарь
«Генеральная пассажирская компания» запускает новогодние железнодорожные экскурсии из Санкт-Петербурга в Великий Устюг. Для всех покупателей этой поездки разработали особенный подарок — адвент-календарь.
Адвент-календарь представляет собой коробку в виде главного перевозчика «Генеральной пассажирской компании» — двухэтажного вагона. В коробке в два уровня лежат коробочки, в каждой коробочке по конфете. На верхнем уровне находится \(n\) коробочек, на нижнем уровне находится \(m\) коробочек. На каждой коробочке написано натуральное число от \(1\) до \(n+m\) включительно. Числа на коробочках не повторяются.
Для каждой коробочки известна её длина. Коробочки могут отличаться по длине. Гарантируется, что суммы длин коробочек на первом и втором уровнях адвент-календаря совпадают.
Чтобы правильно открыть адвент-календарь, нужно в первый день вытащить и открыть коробочку с номером \(1\), во второй день — коробочку с номером \(2\) и так далее, завершает календарь коробочка с номером \(n+m\), которую следует вытащить и открыть в \((n+m)\) по счёту день. Пример адвент-календаря на рисунке.
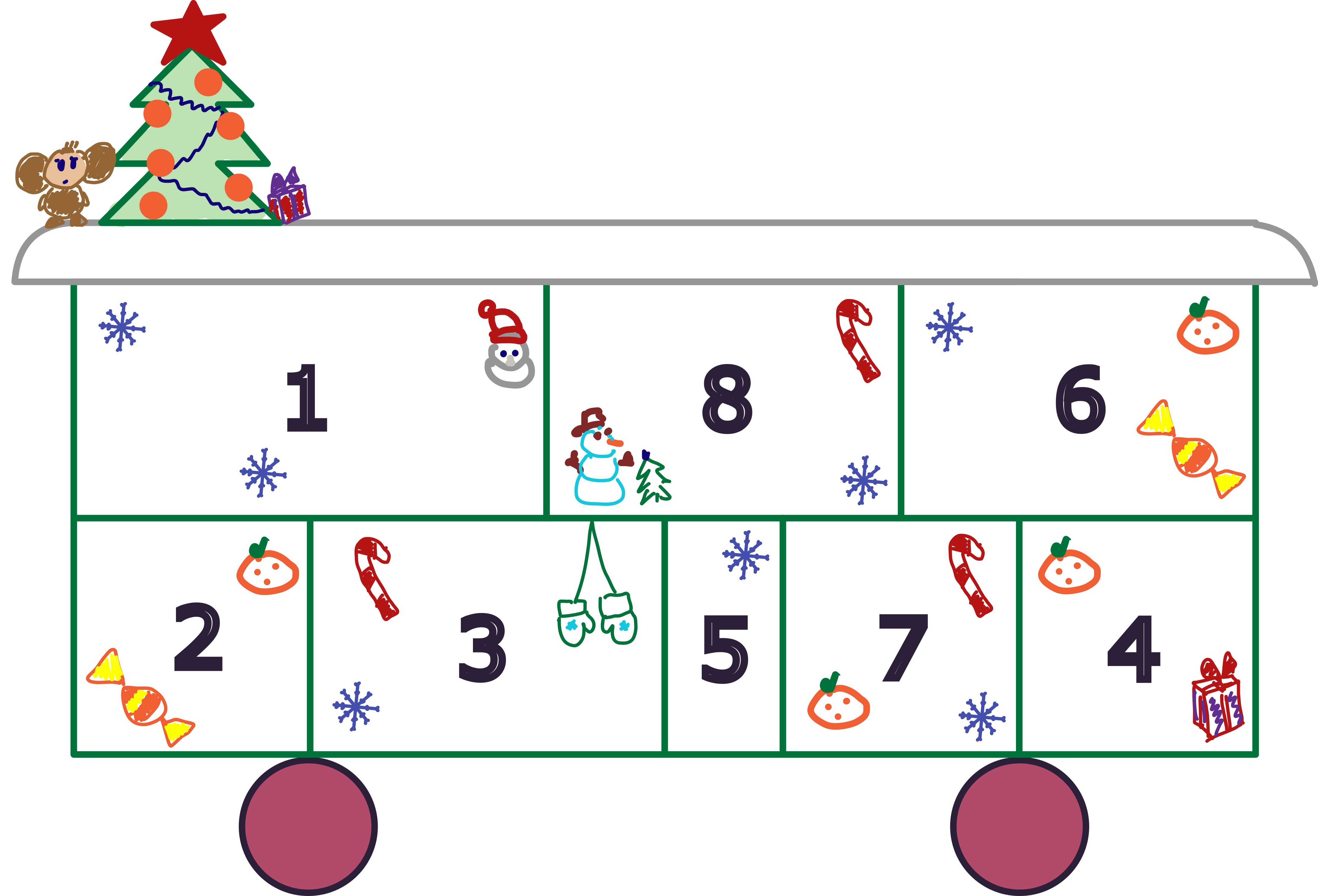Адвент-календарь на \(8\) ячеек. Чтобы правильно открыть его и создать новогоднее настроение, за \(8\) дней до Нового года нужно открыть ячейку \(1\), за \(7\) дней ячейку \(2\) и так далее. В последний день — 31 декабря — нужно открыть ячейку \(8\).
Дизайнер и перфекционист Майя решила прокатиться на Новый год в поезде и получила в подарок двухэтажный адвент-календарь. Майя считает неудобным, когда она открывает коробочку с конфетой на нижнем уровне, а сверху на ней на верхнем уровне лежит хотя бы одна ещё не открытая коробочка.
Майе стало интересно, сколько коробочек заранее нужно вытащить из календаря, чтобы он стал удобным. При этом Майе хочется, чтобы в адвенте осталось как можно больше коробочек. Помогите ей ответить, какое минимальное количество коробочек нужно заранее вытащить из календаря, чтобы при открытии коробочки на нижнем уровне на ней не лежала ни одна ещё не открытая коробочка из верхнего уровня. Заранее коробочки можно вытаскивать как с верхнего, так и с нижнего уровня.
На первой строке ввода находится целое число \(n\) (\(1 \le n \le 10^{5}\)) — количество коробочек на верхнем уровне календаря.
В следующих \(n\) строках находятся два числа \(a_i\) и \(x_i\) (\(1 \le a_i \le 10^{9}\), \(1 \le x_i \le n + m\)) — длина \(i\)-й слева коробочки на верхнем уровне календаря и номер, который на ней написан, соответственно.
На \((n+1)\) строке ввода находится целое число \(m\) (\(1 \le m \le 10^{5}\)) — количество коробочек на втором уровне календаря.
В следующих \(m\) строках находятся два числа \(b_j\) и \(y_j\) (\(1 \le b_j \le 10^{9}\), \(1 \le y_j \le n + m\)) — длина \(j\)-й слева коробочки на нижнем уровне календаря и номер, который на ней написан, соответственно. Гарантируется, что \(a_1 + a_2 + \ldots + a_n = b_1 + b_2 + \ldots + b_m\). Гарантируется, что все числа в множестве \(\{x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_m\}\) различны.
Выведите единственное число \(k\) — минимальное количество коробочек, которые надо достать из календаря, чтобы он стал удобным.
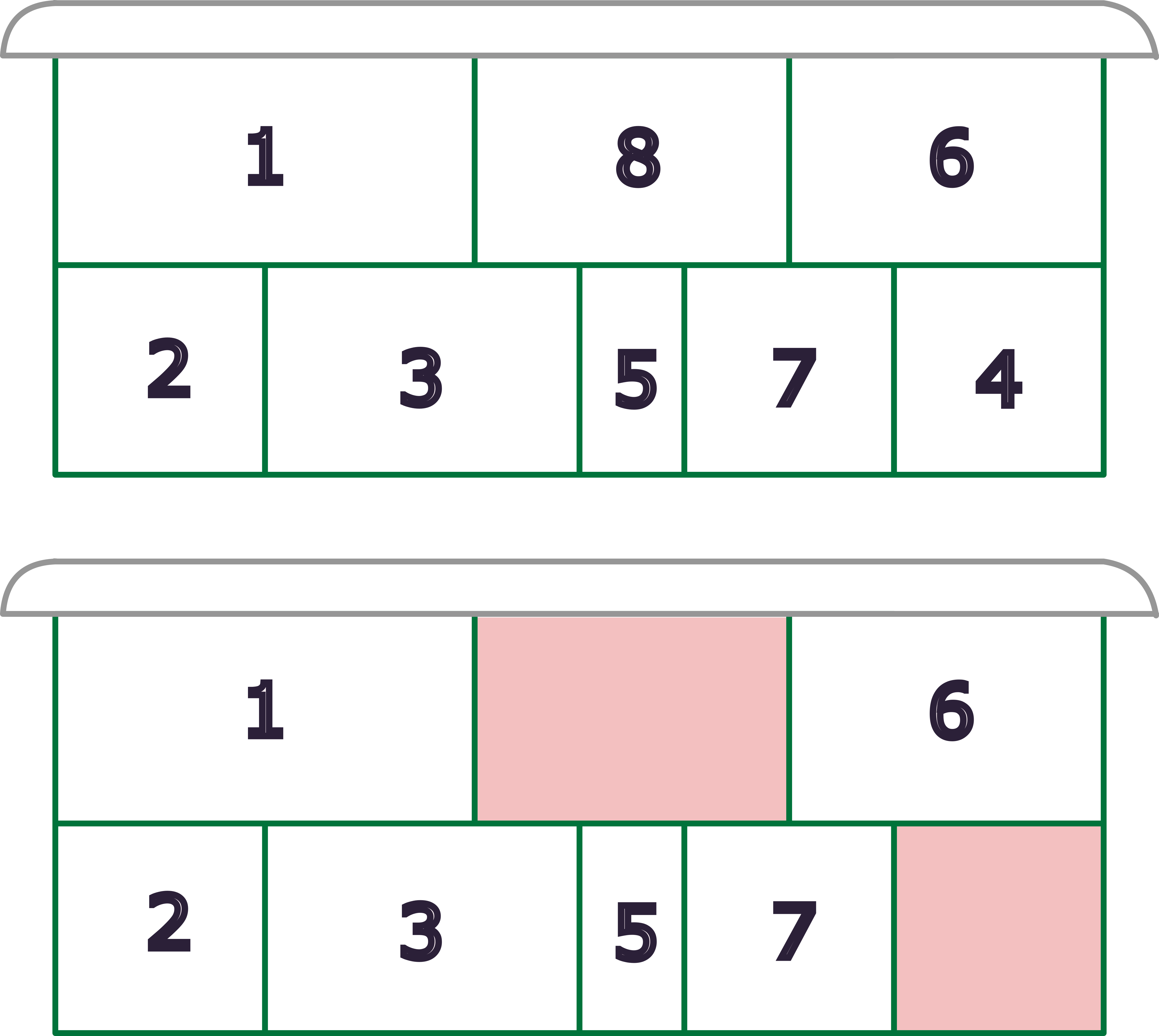
Во втором примере можно убрать коробки с номерами \(4\) и \(8\). После этого календарь будет выглядеть как на рисунке ниже и станет удобным.
3 1 1 1 2 1 3 3 1 4 1 5 1 6
0
3 4 1 3 8 3 6 5 2 2 3 3 1 5 2 7 2 4
2