Задача №115431. Промежуточная вертикальность
Два классических алгоритма на графах — обход в глубину и обход в ширину — строят в графе два остовных дерева. При этом обход в глубину известен тем, что в полученном дереве нет горизонтальных рёбер — рёбер, соединяющих вершины, которые не являются предками друг друга, а обход в ширину — тем, что в полученном дереве нет вертикальных рёбер — рёбер, соединяющих вершину с предком в дереве. В этой задаче вам понадобится построить промежуточное остовное дерево, имеющее заданное число горизонтальных и вертикальных рёбер.
Напомним, что неориентированный граф состоит из множества вершин \(V\) и множества рёбер \(E\), где каждое ребро соединяет две вершины. Будем рассматривать связные графы, то есть такие графы, в которых можно от любой вершины добраться до любой другой по рёбрам. Дерево — это связный неориентированный граф, не содержащий циклов, а остовное дерево в графе — подмножество его рёбер, которое образует дерево, по которому можно добраться от любой вершины графа до любой другой. Напомним два основных свойства дерева: в дереве с \(n\) вершинами ровно \(n-1\) рёбер, а между любыми двумя вершинами в дереве есть ровно один путь.
Выделим в графе вершину \(r\), которую будем называть корнем дерева. Вершины, которые лежат на единственном пути от вершины \(x\) до вершины \(r\), называются предками вершины \(x\), а первая вершина на этом пути называется родителем вершины \(x\) и обозначается как \(p_x\). У корня родителя нет.
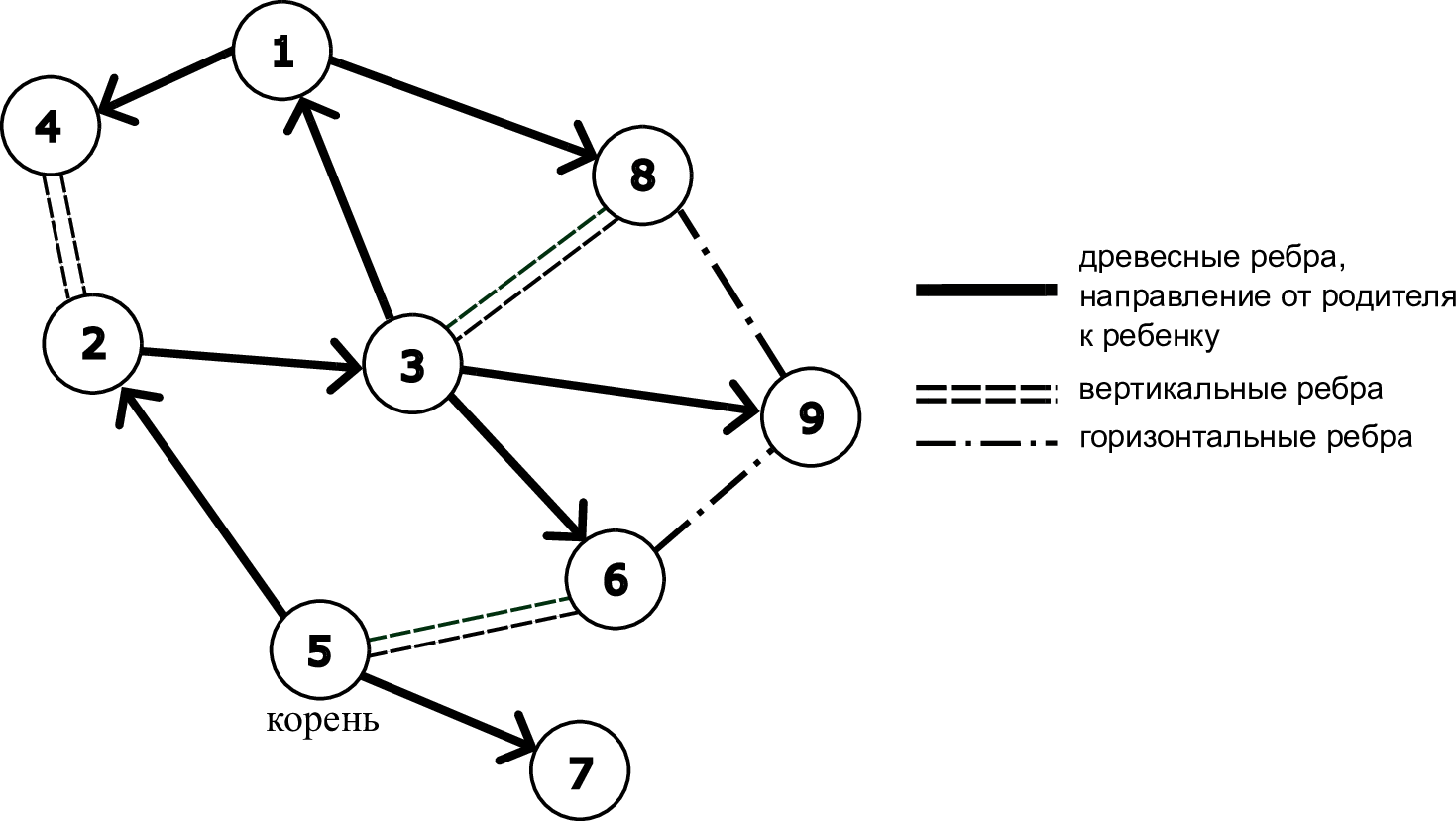
Если в графе зафиксирован корень и остовное дерево, то все рёбра графа можно разделить на три типа:
- древесные — рёбра выбранного остовного дерева;
- вертикальные — рёбра, не принадлежащие дереву, соединяющие вершину с её предком;
- горизонтальные — остальные рёбра графа.
Вам задан граф с \(n\) вершинами и \(m\) рёбрами, корень дерева \(r\) и число \(h\), \(0 \le h \le m-n+1\). Необходимо построить остовное дерево заданного графа с корнем в \(r\), имеющее вертикальность, равную \(h\), либо сообщить, что такого дерева не существует.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число \(t\) — количество наборов входных данных (\(1 \le t \le 10^5\)). Далее следуют одно за другим описания \(t\) наборов входных данных.
В первой строке каждого набора входных данных находится четыре целых числа \(n\), \(m\), \(r\) и \(h\) — количество вершин и рёбер в графе, соответственно, номер корневой вершины и требуемая вертикальность будущего остовного дерева (\(2 \le n \le 3 \cdot 10^5\); \(n - 1 \le m \le 3 \cdot 10^5\); \(1 \le r \le n\); \(0 \le h \le m - n + 1\)).
В каждой из следующих \(m\) строк находится по два целых числа \(u_i\), \(v_i\) — номера вершин, соединённых ребром в графе (\(1 \le u_i, v_i \le n\); \(u_i \ne v_i\)).
Гарантируется, что все графы связные, не содержат петель и кратных рёбер. Гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(3 \cdot 10^5\). Гарантируется, что сумма \(m\) по всем наборам входных данных не превосходит \(3 \cdot 10^5\).
Для каждого тестового случая найдите требуемое остовное дерево \(T\) и выведите в отдельной строке \(n\) целых чисел \(p_1, p_2, \ldots, p_n\), где \(p_i\) — номер родителя \(i\)-й вершины в дереве \(T\) (\(1 \le p_i \le n\)). В качестве \(p_r\) можете вывести любое число от \(1\) до \(n\). Если дерева \(T\), обладающего нужными свойствами, не существует, выведите вместо этого \(n\) чисел \(-1\).
4 5 7 2 0 1 2 2 3 3 4 4 1 3 5 5 4 1 5 5 7 2 1 1 2 2 3 3 4 4 1 3 5 5 4 1 5 5 7 2 2 1 2 2 3 3 4 4 1 3 5 5 4 1 5 5 7 2 3 1 2 2 3 3 4 4 1 3 5 5 4 1 5
2 1 2 3 3 2 1 4 1 1 2 1 5 5 1 2 1 4 1 3