Задача №115446. Робот-доставщик
Прогрессивная бургерная «ITБургер» планирует запустить доставку своих бургеров с помощью автономных роботов-доставщиков, которые умеют самостоятельно планировать оптимальный маршрут доставки.
Для того, чтобы обучать робота, инженер Альбина построила испытательный полигон, который представляет собой координатную плоскость. В узлах координатной плоскости нанесено \(n \times n\) световых меток в виде квадрата, соседние по столбцу и строке метки находятся на единичном расстоянии друг от друга. Левая нижняя метка находится в узле с координатами \((0,0)\), а правая верхняя — в узле с координатами \((n - 1, n - 1)\).
Цель робота — построить маршрут, чтобы посетить все световые метки. Робот может начать движение в любой точке координатной плоскости с целыми координатами от \(-1000\) до \(1000\). Он может двигаться только по прямой, поэтому его траекторией будет ломаная линия. Альбина считает, что робота можно запрограммировать так, чтобы он обошёл световые метки маршрутом в виде ломаной линии, содержащей ровно \(2n - 2\) отрезков, причем начало и конец маршрута, а также все повороты будут в точках с целыми координатами от \(-1000\) до \(1000\). Помогите роботу найти такой маршрут.
В первой строке ввода находится единственное целое число \(n\) (\(3 \le n \le 100\)) — количество световых меток в одной строке квадрата.
Выведите \(2n - 1\) пар целых чисел — маршрут робота. Первая пара чисел — координата точки начала маршрута, следующие \(2n - 3\) пары чисел — точки, в которых робот делает поворот, последняя пара чисел — координаты конца маршрута.
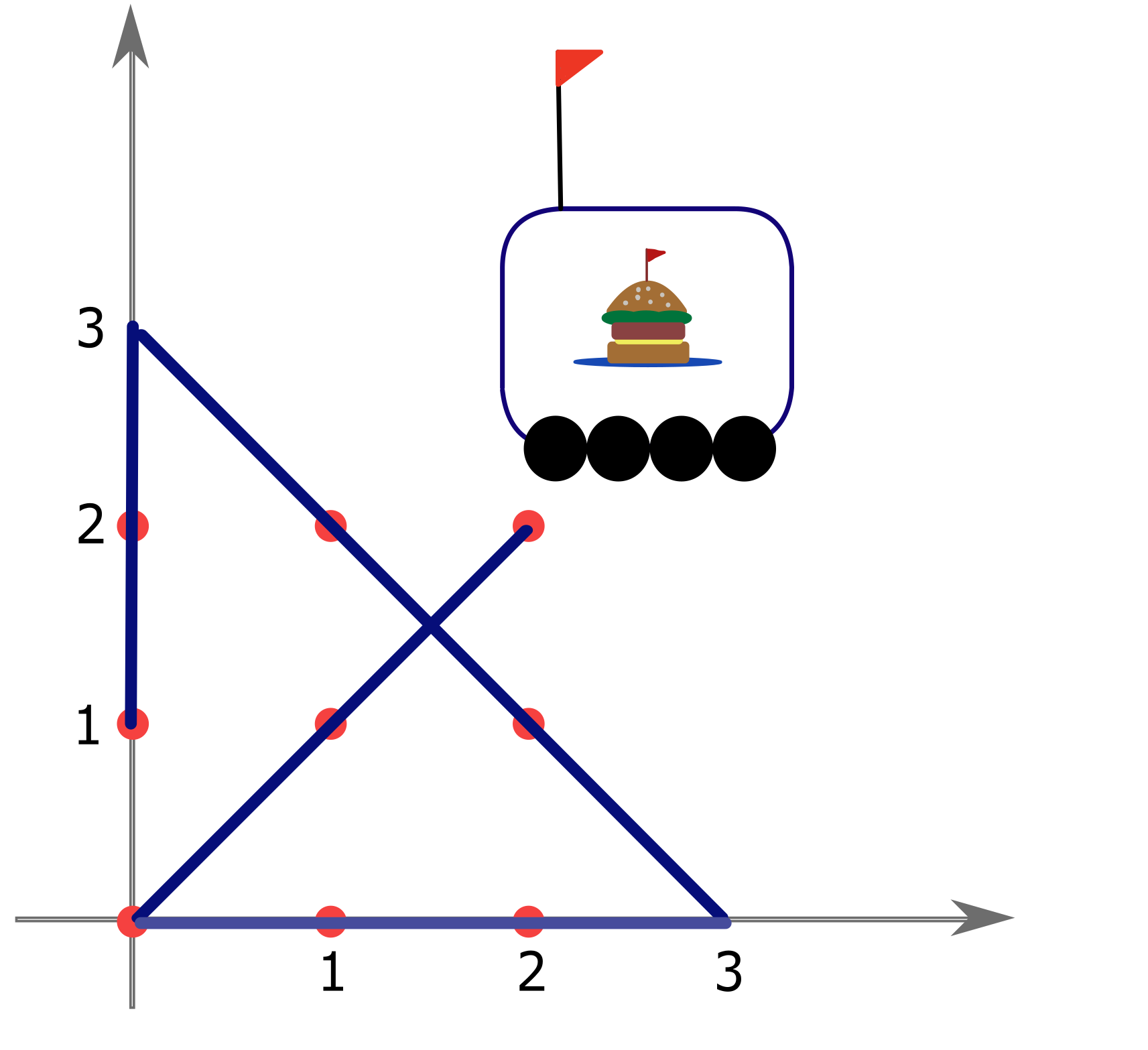
Маршрут робота при \(n = 3\). Робот может начать в точке \((2, 2)\) и закончить в точке \((0, 1)\). Его траектория показана на рисунке.
3
2 2 0 0 3 0 0 3 0 1