Задача №1394. Горный туризм
Клуб активного туризма на планете Олимпия решил предложить клиентам маршрут вдоль живописного хребта. Хребет достаточно длинный и его трудно пройти сразу, поэтому в клубе ищут самый привлекательный из маршрутов ограниченной длины. Согласно результатам социального исследования туристы любят проходить по местам, которые выше чем другие на как можно большем промежутке, благодаря более широкому обзору и эйфории от ощущения высоты.
Для упрощения задачи хребет разделили на однометровые отрезки и определили среднюю высоту над уровнем моря каждого из них. Численное значение привлекательности каждого такого отрезка хребта равно количеству последовательных отрезков слева и справа, начиная с непосредственных его соседей, которые имеют высоту строго меньшую чем он сам. Сам отрезок в эту сумму не входит. Привлекательность маршрута вычисляется как сумма привлекательностей однометровых отрезков хребта, которые в него входят. Длина маршрута должна быть не больше чем T метров. Направление маршрута значения не имеет, поскольку не меняет его привлекательности. Маршрут может начинаться с любого отрезка хребта. Маршрут не может содержать разрывов, то есть в маршрут можно включать только последовательные отрезки хребта.
Напишите программу, которая по информации о высоте над уровнем моря каждого однометрового отрезка горного хребта вычислит привлекательность наиболее привлекательного маршрута длины не больше чем T метров.
Первая строка входного файла содержит два целых числа N – длина всего хребта в метрах и T (1≤T≤N≤100 000) – ограничение на длину маршруту. Вторая строка файла содержит N целых чисел от 1 до 106 – высоты последовательных однометровых отрезков.
Единственная строка выходного файла должна содержать одно целое число – численное значение привлекательности самого привлекательного маршрута вдоль горного хребта длины не более чем T.
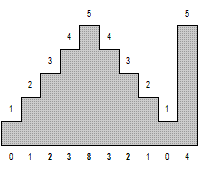
На рисунке изображен хребет, который соответствует входным данным, разбитый на 10 отрезков. Числа сверху соответствуют высоте каждого из отрезков, а числа снизу – привлекательности соответствующего отрезка.
Решения, работающие для случая \(NT < 4 \cdot 10^6\) будут оцениваться из 40 баллов
10 5 1 2 3 4 5 4 3 2 1 5
18