Статистика решения: 10,98% участников полностью решили задачу, 42,68% набрали 0 баллов.
Решение задачи:
Для решения задачи необходимо использовать двумерный массив board. Элемент массива board[x][y] хранит минимальное расстояние, за которое можно добраться от клетки с координатами (x; y) до кормушки (S; T). Элемент этого массива не превысит значения 250, так как блохи прыгают конем, прыгают «в ширь», а также не прыгают на уже достигнутые клетки. Удобнее решать задачу с конца, то есть находить не расстояние от каждой блохи до кормушки, а расстояние от кормушки до всех потенциальных позиций блох на доске. Рассмотрим решение на первом примере:
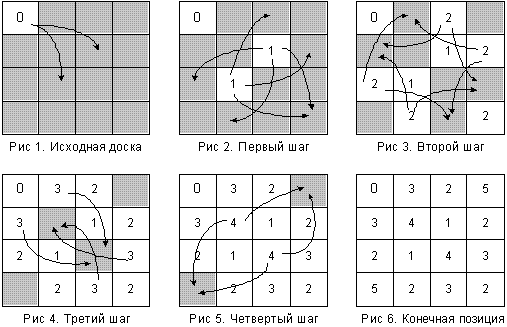
Закрашенные клетки – на текущий момент это не достижимые клетки. В начале работы алгоритма массив board представлен на рис. 1. На первом шаге (рис. 2), по алгоритму волны надо просмотреть возможные пути конем в закрашенные клетки из ячеек, содержащих 0, и присвоить им значение 1. На втором шаге (рис. 3) надо просмотреть все возможные пути конем в закрашенные клетки из ячеек, содержащих 1. Таким образом, каждый раз надо увеличивать длину пути на единицу. В итоге (рис. 6) получена доска, с расстояниями от каждой клетки до кормушки.
Для обоих, рассматриваемых ниже, реализаций этой идеи целесообразно завести массив с запасом на 2 ячейки по горизонтали и по вертикали, пометив их как запретные, чтобы было удобнее контролировать ходы за границу доски.
1 способ. Решение этой задачи сводится к алгоритму волны. Псевдокод будет выглядеть следующим образом:
while <были проведены изменения> do begin
for i := 1 to N do
for j := 1 to M do
if board[i][j] = <текущий шаг> then
<незанятые клетки «на расстоянии коня»> := <текущий шаг> + 1;
<увеличить текущий шаг>;
end;
Осталось только посчитать сумму длин путей. Сложность этого алгоритма порядка
2 способ. Очевидна неэффективность первого способа. Применение очереди дает значительный выигрыш, а сложность алгоритма будет оцениваться . Суть заключается в следующем:
изначально в очередь ставиться клетка с координатами кормушки, board[S][T] присваивается 0;
взять из очереди следующий элемент, далее по порядку заполняются незанятые клетки «на расстоянии коня» в board и одновременно, в случае заполнения, эта клетка ставиться в очередь;
делать пункт 2 пока очередь не пуста.
Блохи сидят на клетках шахматного поля и ходят конем. Должны собраться в одной из клеток. Определить сумму длин кратчайших путей.
На клеточном поле, размером \(N\)x\(M\) (2 ≤ \(N\), \(M\) ≤ 250) сидит \(Q\) (0 ≤ \(Q\) ≤ 10000) блох в различных клетках. "Прием пищи" блохами возможен только в кормушке - одна из клеток поля, заранее известная. Блохи перемещаются по полю странным образом, а именно, прыжками, совпадающими с ходом обыкновенного шахматного коня. Длина пути каждой блохи до кормушки определяется как количество прыжков. Определить минимальное значение суммы длин путей блох до кормушки или, если собраться блохам у кормушки невозможно, то сообщить об этом. Сбор невозможен, если хотя бы одна из блох не может попасть к кормушке.
Выходные данные
Содержит одно число - минимальное значение суммы длин путей или -1, если сбор невозможен.