Задача №1808. Затопление
Многоугольник топят в жидкости, опуская его из воздуха с постоянной скоростью v метров в минуту. Жидкость разъедает многоугольник со всех сторон с постоянной скоростью c метров в минуту. Для точки (\(x\), \(y\)) внутри многоугольника, опускающейся вместе с ним, выясните, в какой момент разъедающая жидкость доберётся до этой точки.
Граница между воздухом и жидкостью проходит по прямой \(y\)=0. Жидкость разъедает многоугольник как двумерную фигуру. Многоугольник не поворачивается при опускании в жидкость, и в момент времени 0 он не касается жидкости.
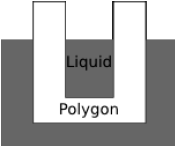
В отличие от многоугольника, который считается двумерным, жидкость существует в трёх измерениях. Поэтому она проникает внутрь «дыр» в многоугольнике. Например, если многоугольник имеет форму «чашки», жидкость проникает «внутрь», как показано на рисунке.
В первой строке входного файла записано через пробел пять целых чисел \(n\), \(x\), \(y\), \(v\) и \(c\) (3 \(\le\) \(n\) \(\le\) 30, −100 \(\le\) \(x\) \(\le\) 100, 1 \(\le\) \(y\) \(\le\) 100, 1 \(\le\) \(c\) < \(v\) \(\le\) 100). Следующие \(n\) строк описывают вершины многоугольника; \(i\)-я из них содержит два целых числа \(x\) и \(y\) через пробел (−100 \(\le\) \(x\) \(\le\) 100, 1 \(\le\) \(y\) \(\le\) 100). Вершины даны в порядке обхода против часовой стрелки. Многоугольник не имеет самопересечений и самокасаний, а точка (\(x\), \(y\)) лежит строго внутри него.
Выведите одно число — время, которое потребуется жидкости, чтобы добраться до точки (\(x\), \(y\)), с точностью не менее четырёх знаков после запятой.
4 0 50 2 1 -1 10 1 10 1 90 -1 90
25.8660