Задача №1809. Поворот до корня
Поворот до корня — это одна из эвристик для балансировки двоичных деревьев поиска. В этой задаче содержимое дерева будет игнорироваться, и вас будут интересовать только структурные изменения, произошедшие в результате применения эвристики.
Эта эвристика работает следующим образом при вызове от некоторого узла X. Пока X не является корнем дерева, применяется такая процедура:
* Если X — левый ребёнок своего родителя, производится правый поворот дерева.
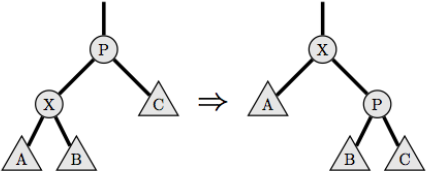
* Если X — правый ребёнок своего родителя, производится левый поворот дерева.
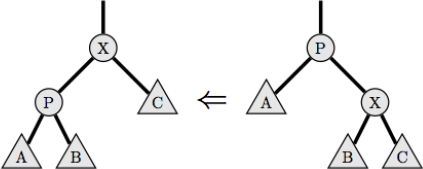
Ясно, что повороты сохраняют порядок элементов в дереве поиска, именно поэтому их используют, но это неважно для решения этой задачи.
Напишите программу, которая после каждого применения операции поворота до корня выведет высоту дерева после выполнения этой операции.
Входной файл состоит из одного или нескольких тестов. Первая строка каждого теста содержит целое число \(N\) — число узлов в дереве (1 \(\le\) \(N\) \(\le\) \(10^5\)).
Далее следуют \(N\) строк по два числа в каждой, при этом на \(i\)-й строке записаны левый и правый дети \(i\)-й вершины. Нулём обозначаются пустые поддеревья.
Гарантируется, что во вводе задано корректное двоичное дерево.
Входной файл завершается тестом с \(N\)=0, который не нужно обрабатывать.
Общая сумма всех значений \(N\) по всему файлу не превосходит 2 * \(10^5\).
Для каждого теста выведите \(N\) строк — на \(i\)-й строке выведите высоту дерева после применения операции поворота исходного дерева к \(i\)-му узлу.
4 2 3 4 0 0 0 0 0 0
3 3 4 3