Задача №22. Ударим мостом по бездорожью
Профиль Уральских гор задается ломаной (x1, y1), (x2, y2), …, (xN, yN), для координат вершин которой верны неравенства x1 < x2 < … < xN. Начальные и конечные точки профиля расположены на уровне моря (y1 = yN = 0).
На горном профиле заданы две различные точки A и B, между которыми требуется проложить дорогу. Эта дорога будет проходить по склонам гор и проектируемому горизонтальному мосту, длина которого не должна превышать L. Оба конца моста находятся на горном профиле. Дорога заходит на мост с одного конца и выходит с другого. Мост не может содержать точек, расположенных строго под ломаной (строительство тоннелей не предполагается).
|
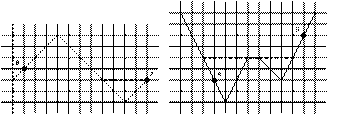
Возможные примеры расположения моста
|
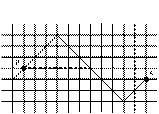
Невозможное расположение моста
|
Достоверно известно, что строительство такого моста в данной местности возможно, причем позволит сократить длину дороги из точки A в точку B. Требуется написать программу, которая определит такое расположение горизонтального моста, что длина дороги от точки A до точки B будет наименьшей.
Первая строка входных данных содержит два целых числа N и L — количество вершин ломаной (2 ≤ N ≤ 100 000) и максимальную длину моста (1 ≤ L ≤ 106) соответственно. Вторая строка содержит координаты точки A, третья строка — координаты точки B. Точки A и B различны.
Последующие N строк содержат координаты вершин ломаной (x1, y1), (x2, y2), …, (xN, yN). Координаты вершин ломаной, а также точек A и B, задаются парой целых чисел, не превосходящих по абсолютному значению 106. Гарантируется, что x1 < x2 < … < xN и y1 = yN = 0, а также, что точки A и B принадлежат ломаной.
В первой и второй строках выходных данных выведите координаты концов моста с точностью не менее 5 знаков после десятичной точки. В случае, когда решений несколько, выведите любое из них.
В примере в первой строке указана длина дороги от точки A до точки B с учётом построенного моста. Её не нужно выводить.
Примечание
Решения, корректно работающие при N ≤ 2000, будут оцениваться, исходя из 80 баллов.
5 3 1 1 3 1 -1 0 0 2 2 0 4 2 5 0
2.000000000 1.00000 1.00000 3.00000 1.00000