Задача №2775. Змейка
Кубик-змейка --- это механическая головоломка, состоящая из \(n^3\) кубиков\(1 \times 1 \times 1\), через которые проходит эластичный шнур. Соседние кубики на шнуре касаются одной гранью и могут свободно вращаться друг относительно друга по оси, перпендикулярной этой грани. Каждые три идущих подряд кубика образуют либо прямую линию, либо угол в \(90\) градусов. Согнуть прямой отрезок змейки в угол или распрямить угол в прямой отрезок нельзя; можно лишь при помощи поворотов выбрать, в какую
из четырёх сторон змейка поворачивает на каждом углу.Цель --- собрать из этой змейки большой куб \(n \times n \times n\).
Пример змейки показан на рисунке.
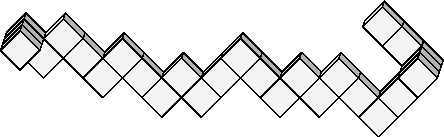
Конечно, не из любой змейки можно собрать куб --- для этого необходимо, как минимум, чтобы все прямые куски змейки состояли не более чем из \(n\) кубиков.
Будем задавать змейку последовательностью длин её прямых кусков, точнее, последовательностью расстояний между центрами первого и последнего кубиков в каждом прямом куске. Например, змейка, показанная на рисунке, задаётся
слева направо следующим образом: 2 1 1 2 1 2 1 1 2 2 1 1 1 2 2 2 2. В этой задаче предлагается решить обобщённую версию этой головоломки. Дана змейка из \(l \cdot w \cdot h\) клеток. Уложите её в прямоугольный параллелепипед размера \(l \cdot w \cdot h\) клеток или выясните, что это невозможно.
В первой строке входного файла записаны через пробел четыре целых числа --- \(l\), \(w\), \(h\) и \(m\)
(\(1 \leq l, \, w, \, h \leq 4; \, 0 \leq m < l w h\)); здесь \(l\), \(w\) и \(h\) --- это длина, ширина и высота параллелепипеда, соответственно, а \(m\) --- количество звеньев в змейке. Во второй строке записаны \(m\) целых чисел через пробел --- последовательность положительных длин прямых кусков змейки. Гарантируется, что данная змейка содержит ровно \(l \cdot w \cdot h\) кубиков.
Если данную змейку в параллелепипед уложить невозможно, выведите "Bit" в первой строке выходного файла. В противном случае в первой строке входного файла выведите "Baba", а в следующих \(l \cdot w \cdot h\) строках --- координаты кубиков змейки, по три числа на строке. Змейку следует выводить с того же конца, с которого она начинается во входном файле. Числа \(x_i\), \(y_i\) и \(z_i\) в \((i + 1)\)-й строке должны удовлетворять неравенствам \(0 \leq x_i < l\), \(0 \leq y_i < w\) и \(0 \leq z_i < h\). Кроме того, все кубики параллелепипеда \(l \cdot w \cdot h\) должны встретиться в выходном файле по одному разу, в соседних строках должны быть соседние кубики, а повороты должны в точности соответствовать поворотам змейки. Змейка может начинаться и заканчиваться в любом кубике параллелепипеда. Если решений несколько, разрешается выводить любое из них.
3 3 3 17 2 1 1 2 1 2 1 1 2 2 1 1 1 2 2 2 2
Baba 0 0 0 1 0 0 2 0 0 2 1 0 1 1 0 1 1 1 1 1 2 1 2 2 1 2 1 1 2 0 2 2 0 2 2 1 2 1 1 2 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 2 0 0 2 1 0 2 2 0 1 2 0 0 2 1 0 2 2 0 2 2 1 2 2 2 2