Задача №2905. Скользящая симметрия
Движением плоскости называют такое преобразование плоскости, которое сохраняет попарные расстояния между точками, то есть если \(A_1\) и \(B_1\) – образы некоторых точек \(A\) и \(B\) при движении, то \(|A_1 B_1| = |AB|\).
Одной из разновидностей движения плоскости является скользящая симметрия. Скользящей симметрией называют композицию симметрии относительно некоторой прямой \(l\) и переноса на вектор, параллельный \(l\) (этот вектор может быть нулевым). На рисунке показан пример применения скользящей симметрии к отрезку.
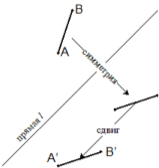
Известно, что любой отрезок можно перевести в любой другой отрезок такой же длины с помощью скользящей симметрии. Требуется по координатам двух различных точек \(A\) и \(B\) и двух точек \(A_1\) и \(B_1\), находящихся на таком же расстоянии друг от друга, как и точки \(A\) и \(B\), найти скользящую симметрию, переводящую точку \(A\) в точку \(A_1\), а точку \(B\) в точку \(B_1\).
В первой строке входного файла находятся четыре целых числа – координаты двух различных точек \(A\) и \(В\). Во второй строке также находятся четыре целых числа – координаты двух различных точек \(A_1\) и \(В_1\). Гарантируется, что \(|A_1B_1| = |AB|\). Все числа во входном файле по модулю не превышают \(1000\). Числа в строках разделены пробелом.
Выведите в выходной файл описание искомой скользящей симметрии, которое представляется в следующем виде.
В первой строке должны выводиться координаты двух различных точек, лежащих на прямой \(l\), относительно которой выполняется симметрия, а во второй – координаты вектора, параллельного этой прямой, на который осуществляется перенос. Вещественные числа должны быть представлены не менее чем с 6 знаками после десятичной точки.