Расположим числа в виде треугольника следующим образом. По левому и правому краю будут стоять единицы, а сумма двух рядом стоящих на одной строке чисел будет давать число, находящееся на одну строку ниже между ними. С помощью определенной строки такого треугольника, который носит название треугольника Паскаля, можно найти коэффициенты разложения (a + b)ⁿ.

Например:

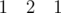
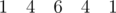
(a + b)² = 1a² + 2ab + 1b²

(a + b)³ = 1a³ + 3a²b + 3ab² + 1a³

(a + b)⁴ = 1a⁴ + 4a³b + 6a²b² + 4ab³ + 1b⁴

Требуется при заданном N найти наибольший коэффициент в разложении (a + b)ⁿ.