Задача №3371. Автостоянка
Олимпиада завершена. Режим дорешивания.
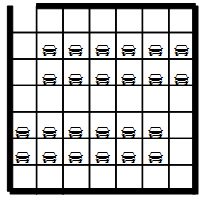
Автостоянка в Цветочном городе представляет собой прямоугольник \(N\times M\) клеток, в каждую из которых можно поставить машину. Стоянка обнесена забором, одна из сторон угловой клетки удалена (это ворота). Машина ездит по дорожке шириной в одну клетку. Незнайку попросили разместить как можно больше машин на стоянке таким образом, чтобы любая машина могла выехать, когда все прочие стоят. Например, на рисунке справа показано, как можно расположить 24 машины на стоянке размером \(7\times 7\). Помогите Незнайке решить эту задачу.
Входные данные
Во входном файле записано два натуральных числа N и M, не превосходящие 7.
Выходные данные
Выведите в выходной файл единственное число: максимальное количество машинок, которое можно расставить на стоянке данного размера.
Примеры
Входные данные
1 3
Выходные данные
1
Входные данные
2 2
Выходные данные
2
Сдать: для сдачи задач необходимо войти в систему