Задача №3372. Жадная волна
Поле размером \(N\times M\) клеток заполнено целыми числами. Требуется найти на поле клетку, из которой волна, запущенная не более чем на \(K\) итераций, покроет площадь с максимальной суммой расположенных на ней чисел.
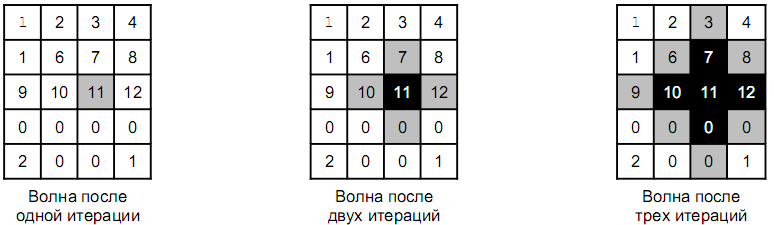
Пример распространения волны для поля размером \(5\times 4\). Волна запущена из клетки (3, 3) и была остановлена после трех итераций. Белые клетки – клетки, не покрытые волной, серые и черные – клетки, покрытые волной. Клетки, покрытые волной на последней итерации, отмечены серым цветом.
В первой строке входного файла содержатся три целых числа через пробел \(N\), \(M\) и \(K\) (\(1 \leq N, M \leq 100\), \(1 \leq K \leq N + M\)). Следующие \(N\) строк содержат по \(M\) чисел, каждое из которых не превосходит \(10000\) по абсолютной величине.
Выведите четыре числа \(R\), \(C\), \(P\) и \(S\), где \(R\) – номер строки, \(C\) – номер столбца, из которых следует запустить волну, \(P\) – количество итераций распространения волны, \(S\) – максимальная сумма чисел, покрытых волной. Если существует несколько вариантов ответа, то вывести любой, в котором число \(P\) минимально. \(1 \leq P \leq K\).
Решение, верно работающее при \(N, M \leq 15\) будет получать 50 баллов. Эти баллы выставляются при прохождении всех тестов группы. В оставшихся тестах \(N, M \leq 100\), эта группа оценивается при прохождении всех тестов группы.
5 4 3 1 2 3 4 1 6 7 8 9 10 11 12 0 0 0 0 2 0 0 1
3 3 3 66