Задача №3630. Распил
Когда Петя учился в младших классах, он любил заниматься выпиливанием лобзиком из фанеры различных фигурок. Чтобы можно было заново выпилить наиболее интересные варианты, каждый раз делая распил, он записывал в свою тетрадку, какую фигуру он распилил на какие части.
Недавно Петя нашел у себя в тетрадке запись, из которой следовало, что он распилил n-угольник вдоль прямой, проходящей через две его вершины. В результате распила образовалось ровно две части, одна из которых — k-угольник, а другая — m-угольник. Петя заинтересовался, каким образом такое могло получиться.
Помогите Пете, постройте n-угольник и укажите в нем две различные вершины A и B таким образом, чтобы при распиле n-угольника вдоль прямой AB, получилось ровно два многоугольника, один из которых является k-угольником, а другой — m-угольником.
Входной файл содержит три целых числа: n, m и k (3 ≤ n, m, k ≤ 200).
Если описанная в условии ситуация могла иметь место, выведите на первой строке выходного файла слово «Yes». В этом случае затем следует вывести пример многоугольника и распила. Следующие n строк должны содержать по два целых числа — координаты вершин многоугольника в порядке обхода. Координаты не должны превышать 104 по модулю. Граница многоугольника не должна иметь самопересечений и самокасаний. Никакие три подряд идущие вершины многоугольника не должны лежать на одной прямой.
Будем считать вершины пронумерованными от 1 до n в порядке, в котором они выведены. Последняя строка должна содержать два числа: номера вершин, через которые был проведен распил.
Если описанная в условии ситуация невозможна, выведите на первой строка выходного файла слово «No».
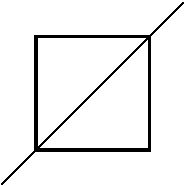
Рисунок ко второму примеру 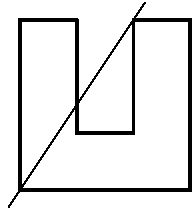
4 3 3
Yes 0 0 1 -4 1000 0 999 4 1 3
8 4 7
Yes 0 0 1 -4 1 -5 999 1 1000 0 999 4 999 5 998 4 1 5