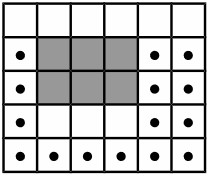
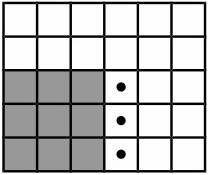
Задача №3817. Поле для игры
Петя создает поле для своей новой игры. Поле разделено на клетки и представляет собой прямоугольник размером N на M клеток. Пусть клетки имеют координаты от 1 до N слева направо по горизонтали и от 1 до M снизу вверх по вертикали.
На этом поле Петя уже разместил супермаркет, который представляет собой прямоугольник размером C на D клеток (C –– размер по горизонтали, D –– по вертикали), и нижняя левая клетка супермаркета имеет координаты A, B на игровом поле (см. примеры и рисунки). Теперь Пете нужно разместить на том же игровом поле здание биржи. Здание биржи представляет собой прямоугольник размером E на F клеток (E –– по горизонтали, F –– по вертикали). Естественно, что здание биржи должно полностью располагаться на игровом поле и не должно иметь общих клеток с супермаркетом (но может касаться его).
Сколькими способами Петя сможет разместить здание биржи?
Вводятся числа N, M, A, B, C, D, E, F, каждое в отдельной строке. Числа удовлетворяют следующим условиям: 1 ≤ N ≤ 100, 1 ≤ M ≤ 100, 1 ≤ A ≤ N, 1 ≤ B ≤ M, 1 ≤ A + C - 1 ≤ N, 1 ≤ B + D - 1 ≤ M, 1 ≤ E ≤ N, 1 ≤ F ≤ M.
Выведите количество способов разместить здание биржи.
6
5
2
3
3
2
1
2
15
4
4
2
2
3
2
2
2
0
6
5
1
1
3
3
3
3
3
Рисунки ниже соответствуют приведенным примерам. На рисунках серым показано здание супермаркета. Точками отмечены варианты размещения нижнего левого угла здания биржи.