Задача №413. Раскраска в три цвета
Петя нарисовал на бумаге n кружков и соединил некоторые пары кружков линиями. После этого он раскрасил каждый кружок в один из трех цветов – красный, синий или зеленый.
Теперь Петя хочет изменить их раскраску. А именно – он хочет перекрасить каждый кружок в некоторый другой цвет так, чтобы никакие два кружка одного цвета не были соединены линией. При этом он хочет обязательно перекрасить каждый кружок, а перекрашивать кружок в тот же цвет, в который он был раскрашен исходно, не разрешается.
Помогите Пете решить, в какие цвета следует перекрасить кружки, чтобы выполнялось указанное условие.
В первой строке вводятся два целых числа n и m – количество кружков и количество линий, которые нарисовал Петя, соответственно ( 1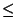 \( le\)" width="16" height="28" align="middle" />n
\( le\)" width="16" height="28" align="middle" />n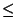 \( le\)" width="16" height="28" align="middle" />1 000, 0
\( le\)" width="16" height="28" align="middle" />1 000, 0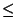 \( le\)" width="16" height="28" align="middle" />m
\( le\)" width="16" height="28" align="middle" />m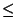 \( le\)" width="16" height="28" align="middle" />20 000).
\( le\)" width="16" height="28" align="middle" />20 000).
Следующая строка содержит n символов из множества {'R', 'G', 'B'} – i-й из этих символов означает цвет, в который раскрашен i-й кружок ('R' – красный, 'G' – зеленый, 'B' – синий).
Далее в m строках задается по два целых числа – пары кружков, соединенных отрезками.
Выведите одну строку, состоящую из n символов из множества {'R', 'G', 'B'} – цвета кружков после перекраски. Если решений несколько, выведите любое.
Если решения не существует, выведите слово "Impossible''.
4 5 RRRG 1 3 1 4 3 4 2 4 2 3
GGBR
4 5 RGRR 1 3 1 4 3 4 2 4 2 3
Impossible