Задача №662. Бассейн реки
 Дана карта рек некоторого континента. Каждая река показана как ломаная линия, которая начинается у истока реки и заканчивается или в точке, где река впадает в другую, или устьем реки. Вершины ломаной - или точки поворота реки, или точки впадения притоков.
Дана карта рек некоторого континента. Каждая река показана как ломаная линия, которая начинается у истока реки и заканчивается или в точке, где река впадает в другую, или устьем реки. Вершины ломаной - или точки поворота реки, или точки впадения притоков.
Будем рассматривать бассейн реки как выпуклый многоугольник минимальной площади, который содержит реку и все её притоки.
Примечание. Согласно этому определению бассейна реки, одна и та же территория может принадлежать бассейнам различных рек.
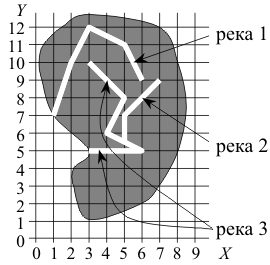
Пример. Показан континент с тремя реками. Координаты рек и площади бассейнов даны в таблице.
| Название реки | x | y | Площадь бассейна реки без притоков |
| река 1 | 6 | 9 | 12,5 |
| 5 | 11 | ||
| 3 | 12 | ||
| 2 | 10 | ||
| 1 | 7 | ||
| река 2 | 7 | 9 | 1,5 |
| 5 | 7 | ||
| 5 | 5,5 | ||
| река 3 | 3 | 10 | 9,5 |
| 5 | 8 | ||
| 4 | 6 | ||
| 5 | 5,5 | ||
| 6 | 5 | ||
| 3 | 5 | ||
Требуется найти максимальную площадь бассейна реки, расположенной на данном континенте.
Первая строка содержит число рек N. В следующих строках файла содержится N блоков, описывающих реки.
Каждый блок номер i состоит:
- из одной строки с ki - числом вершин ломаной, представляющей реку;
- ki строк, содержащих пары вещественных чисел xj и yj (1 <= j <= ki), разделённых пробелом, - координаты точек, описывающих реку.
Ограничения: 1 <= N <= 10, сумма ki <= 1000, -1000 <= xj, yj <= 1000.
Вывести одно число - площадь наибольшего бассейна реки с двумя знаками после запятой.
3 4 6 11 5 13 3 14 1 9 3 7 11 5 9 5 7.5 6 3 12 5 10 4 8 5 7.5 6 7 3 7
16.00