Задача №113891. Канатная дорога
Побывав недавно в лесу, Вася решил построить на деревьях канатную дорогу. Он хочет, чтобы дорога была как можно более длинной, но он плохо помнит высоты деревьев в лесу. К счастью, он уверен, что правильно помнит высоты всех деревьев, кроме, возможно, одного из них.
Известно, что лес состоит из n деревьев, стоящих в ряд и пронумерованных слева направо числами от 1 до n . Высота i -го дерева, по воспоминаниям Васи, равна h i . Канатная дорога длины k должна опираться на k ( 1 ≤ k ≤ n ) деревьев i 1 , i 2 , ..., i k ( i 1 < i 2 < ... < i k ), таких что их высота возрастает, то есть, h i 1 < h i 2 < ... < h i k .
Петя тоже был в лесу, и у него есть q предположений о том, где именно ошибается Вася. Его i -е предположение задаётся числами a i и b i , означающими, что, по мнению Пети, высота дерева с номером a i на самом деле равна b i . Обратите внимание, Петины предположения независимы между собой.
Ваша задача состоит в том, чтобы для каждого предположения Пети найти максимальную длину канатной дороги, которую можно построить с опорой на эти деревья.
Отметим, что в рамках данной задачи длиной дороги Вася считает количество опорных деревьев в ней.
Первая строка входных данных содержит два числа n и m ( 1 ≤ n , m ≤ 400 000 ) — количество деревьев в лесу и количество предположений Пети соответственно.
В следующей строке содержатся n целых чисел h i ( 1 ≤ h i ≤ 10 9 ) — высоты деревьев по предположению Васи.
Каждая из следующих m строк содержит по два целых числа a i и b i ( 1 ≤ a i ≤ n , 1 ≤ b i ≤ 10 9 ).
Для каждого предположения Пети выведите в отдельной строке одно число — максимальную длину канатной дороги.
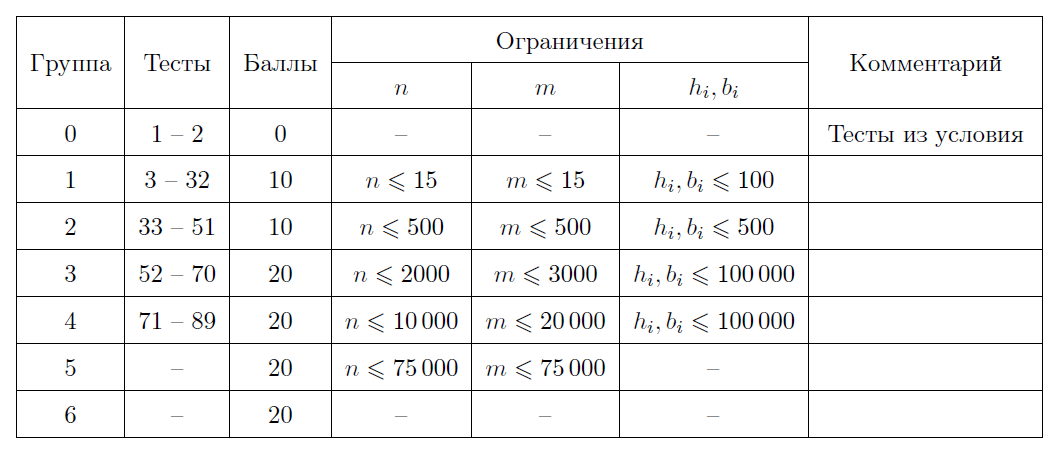
Тесты к этой задаче состоят из семи групп. Баллы за группы ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
Рассмотрим первый пример. Первое Петино предположение совпадает с предположением Васи. Согласно его второму предположению, высоты деревьев были (4, 2, 3, 4) , третьему (1, 2, 3, 3) , а по четвёртому предположению — (1, 2, 3, 5) .
4 4 1 2 3 4 1 1 1 4 4 3 4 5
4 3 3 4
4 2 1 3 2 6 3 5 2 4
4 3