чемпионаты Спб: Чемпионат СПб 2000

Известно, что в книгах для слепых для обозначения различных букв используются различные комбинации выступов, которые читающий различает на ощупь. Пусть для обозначения буквы используется прямоугольник шириной M мм и высотой N мм, причем некоторые входящие в него квадратики размера 1∙1 содержат выступ.

Поскольку слепой не видит границ прямоугольника, то он не может различить комбинации, получающиеся друг из друга сдвигом. Так, он не может различить комбинации а) и б) на рисунке 1. (В то же время комбинации а) и в) являются различимыми, поскольку не могут быть получены друг из друга сдвигом)

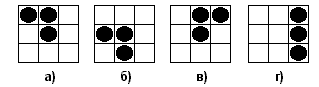
Рисунок 1.

Из-за этого при разработке алфавита для слепых появилась проблема: сколько различных букв можно представить с помощью выступов, если запрещается сопоставлять различным буквам комбинации, получающиеся друг из друга сдвигом. Прямоугольник совсем без выступов также нельзя использовать в качестве буквы (поскольку при написании слова между некоторыми буквами может появиться такой прямоугольник, например между а) и г) на рисунке 1).

Требуется подсчитать количество различных букв, которые можно представить таким способом, если прямоугольник имеет размер M∙N.

В качестве примера, все буквы размера 2∙2 приведены на рисунке 2. (Среди комбинаций, отвечающих одной букве, приведена только одна)

Рисунок 2.