Задача №115176. Ферзь
Пётр любит шахматы и математику. Он знает, что самая мощная фигура в шахматах — это ферзь, потому что он ходит и как ладья, на все клетки на одной с ним вертикали или горизонтали, и как слон, на все клетки по диагоналям. Ферзя можно поставить на доску \(8\times 8\) так, чтобы он контролировал (то есть мог переместиться в эти клетки за один ход) целых 27 клеток доски!
Петра заинтересовало, какое максимальное количество клеток может контролировать ферзь на прямоугольных досках самых разных размеров. Помогите ему в решении этой задачи.
Первая строка входных данных содержит целое число \(n\) (\(1 \le n \le 10^{9}\)) — размер доски по вертикали.
Вторая строка входных данных содержит целое число \(m\) (\(1 \le m \le 10^{9}\)) — размер доски по горизонтали.
Программа должна вывести одно целое число — максимальное количество клеток, которое может контролировать ферзь на доске \(n \times m\).
Обратите внимание на то, что ответ в этой задаче может превышать возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип long long в языке C++, тип int64 в Pascal, тип long в Java и C#).
Решения, правильно работающие, когда \(n\) и \(m\) не превоcходят \(10\), будут оцениваться в 40 баллов.
Решения, правильно работающие, когда \(n\) и \(m\) не превоcходят \(500\), будут оцениваться в 80 баллов.
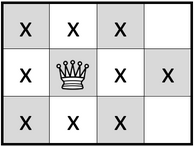
Второй пример из условия приведён на рисунке. Крестиками обозначены клетки, которые контролирует ферзь.
8 8
27
3 4
9