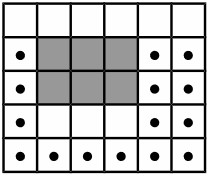
Сегодня мальчик Саша на уроке математики узнал про фракталы. Учитель показывал так называемую «кривую дракона». Она представляет собой геометрическую фигуру, которая строится следующим образом: на первом шаге проводится отрезок из начала координатной плоскости в точку (0; 1). Далее на каждом шаге из конца фрактала повторяется уже нарисованная часть фигуры, повернутая на 90 градусов против часовой стрелки (см. рисунок).
После уроков Саша попробовал сам изобразить «кривую дракона», и теперь он хочет знать, в какой точке координатной плоскости он закончил рисовать фрактал, проделав описанные выше N шагов. Требуется написать программу, которая по заданному числу N определяет координаты конца фрактала после выполнения N шагов.

Вводится одно целое число N (1 ≤ N ≤ 30).
Выведите два числа через пробел — координаты конца фрактала.
2
1 1
4
2 -2
ООО «Симптотика» собирается наладить выпуск обучающих игр для детей младшего дошкольного возраста. Одной из придуманных игр был набор кубиков, из которых можно было собирать различные фигуры. Кубики упаковывались в коробку размером N × N × 1 кубиков.
Однако, многочисленные маркетинговые исследования показали, что детям неинтересно просто собирать различные фигурки. Гораздо интереснее складывать некоторый набор кубиков на дно коробки в столбики, а после этого переворачивать коробку на 90 градусов по часовой стрелке и смотреть, как именно меняется их расположение. Будем для простоты считать, что коробка поворачивается мгновенно, после чего все кубики падают на дно. На следующем рисунке продемонстрировано, как выглядит расположение кубиков в коробке до и после поворота на 90 градусов.

Разумеется, многим детям становится интересно, как будет выглядеть расположение кубиков после K поворотов в том же направлении. Требуется написать программу, которая вычисляет итоговое положение кубиков в коробке после K поворотов.
Сначала вводятся целые числа N и K (1 ≤ N ≤ 10, 0 ≤ K ≤ 109). После этого, во второй строке вводятся N неотрицательных чисел, не превышающих N. i-ое число обозначает количество кубиков в столбце под номером i.
Необходимо вывести N чисел через пробел, i-ое из которых обозначает количество чисел в i-ом столбце в полученном после K поворотов расположении кубиков.
Пример соответствует иллюстрации из условия.
5 1 1 3 4 0 1
4 2 2 1 0
Одна Фруктовая Компания, производящая электронику, решила озаботиться длительностью работы своих смартфонов от аккумулятора.
Выяснилось, что процессор, который они закупают у азиатского поставщика, поддерживает m различных режимов работы, при этом каждая из k операций языка программирования (который Фруктовая Компания использует для написания всех своих программ) может быть выполнена в каждом из режимов. Одновременно процессор может работать только в одном режиме, но перед выполнением каждой из операций можно один раз переключиться в любой другой режим работы.
Известно количество единиц энергии, которое тратится для исполнения каждой из операций в каждом режиме, а также сколько энергии тратится на переключение между режимами. Требуется написать программу, определяющую, какое минимальное количество энергии необходимо потратить для выполнения заданной программы.
В начале выполнения программы процессор находится в первом режиме, завершиться выполнение программы может при любом режиме процессора.
Первая строка содержит три целых числа: число k (1 ≤ k ≤ 100) — количество операций в языке программирования, число m (1 ≤ m ≤ 100) — количество режимов работы, которое поддерживает процессор, и число n (1 ≤ n ≤ 10000) — количество операций в исследуемой программе.
Следующие k строчек содержат по m целых неотрицательных чисел, не превышающих 100. j-е число в i-ой строчке обозначает, сколько энергии тратится на выполнение i-ой операции в j-ом режиме команд.
Далее следует m строчек, содержащих по m целых неотрицательных чисел, не превышающих 100. j-ое число в i-ой строчке обозначает, сколько единиц энергии тратится на переключение процессора с режима i на режим j. Гарантируется, что в i-ой строке i-ое число равно 0.
Последняя строчка содержит исследуемую программу: n натуральных чисел, не превышающих k и соответствующих операциям языка программирования.
Выведите одно число — минимальное количество единиц энергии, необходимое для выполнения программы.
Тесты к этой задаче состоят из трех групп.
- Тесты из условия, оцениваются в ноль баллов.
- В тестах этой группы \(n\), \(m\), \(k\) не превосходят 10. Эта группа оценивается в 50 баллов, баллы ставятся только при прохождении всех тестов группы.
- В тестах этой группы \(m\) не превосходит 10. Эта группа оценивается в 30 баллов, баллы ставятся только при прохождении всех тестов группы и предыдущих групп.
- В тестах этой группы дополнительные ограничения отсутствуют. Группа оценивается в 20 баллов, баллы ставятся только при прохождении всех тестов этой и предыдущих групп.
2 1 4 60 93 0 1 2 1 1
273
2 2 4 1 10 10 1 0 1 2 0 1 1 2 2
5
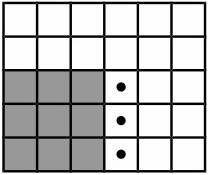
Замок имеет форму большого квадрата, составленного из N × N маленьких квадратиков. Внешние квадратики являются башнями, именно они играют основную роль в защите замка от неприятеля. Например, если замок имеет размер 4 × 4, то у него 12 башен (смотрите второй рисунок, башни на нем выделены серым цветом).
Замок охраняет K полков, которые необходимо разместить по башням. В одной башне можно разместить несколько полков, но при этом в каждой башне должен находиться хотя бы один полк, иначе неприятель легко захватит эту башню. Если все башни защищены, то неприятель выбирает для атаки одну из четырех сторон замка, которую защищает наименьшее число полков (то есть суммарное число полков во всех башнях данной стороны квадрата минимально).
Определите, как нужно разместить полки для наилучшей защиты замка.
Первая строка входных данных содержит число N — размер замка (2 ≤ N ≤ 100). Вторая строка входных данных содержит число K — количество полков, охраняющих замок (0 ≤ K ≤ 100).
Выведите единственное число — количество полков на наименее укрепленной стороне замка при наилучшем размещении полков. Если имеющихся полков недостаточно для защиты всех башен, выведите число 0.
2
5
2
4
15
5
В первом примере башни четыре, а полков пять, поэтому на одну из башен можно поставить два полка, но все равно найдется сторона, которую защищает всего два полка.
Во втором примере можно расположить полки так, что каждую сторону будет защищать 5 полков. Защитить каждую сторону не менее, чем шестью полками не удастся.

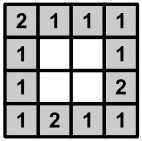
Петя создает поле для своей новой игры. Поле разделено на клетки и представляет собой прямоугольник размером N на M клеток. Пусть клетки имеют координаты от 1 до N слева направо по горизонтали и от 1 до M снизу вверх по вертикали.
На этом поле Петя уже разместил супермаркет, который представляет собой прямоугольник размером C на D клеток (C –– размер по горизонтали, D –– по вертикали), и нижняя левая клетка супермаркета имеет координаты A, B на игровом поле (см. примеры и рисунки). Теперь Пете нужно разместить на том же игровом поле здание биржи. Здание биржи представляет собой прямоугольник размером E на F клеток (E –– по горизонтали, F –– по вертикали). Естественно, что здание биржи должно полностью располагаться на игровом поле и не должно иметь общих клеток с супермаркетом (но может касаться его).
Сколькими способами Петя сможет разместить здание биржи?
Вводятся числа N, M, A, B, C, D, E, F, каждое в отдельной строке. Числа удовлетворяют следующим условиям: 1 ≤ N ≤ 100, 1 ≤ M ≤ 100, 1 ≤ A ≤ N, 1 ≤ B ≤ M, 1 ≤ A + C - 1 ≤ N, 1 ≤ B + D - 1 ≤ M, 1 ≤ E ≤ N, 1 ≤ F ≤ M.
Выведите количество способов разместить здание биржи.
6
5
2
3
3
2
1
2
15
4
4
2
2
3
2
2
2
0
6
5
1
1
3
3
3
3
3
Рисунки ниже соответствуют приведенным примерам. На рисунках серым показано здание супермаркета. Точками отмечены варианты размещения нижнего левого угла здания биржи.