Недавно у градообразующего предприятия города Флатвилля сменилось руководство. Новый генеральный директор не очень-то разбирается в техническом производстве, поэтому заключает все договоры подряд. После этого (чтобы спасти положение) в дело вступает директор по расписаниям, который решает, какие из этих заказов будут выполнены, а за какие придется платить неустойку.
Каждый заказ обладает тремя параметрами: di — максимальный номер дня, к которому этот заказ должен быть выполнен; ai — доход, который получает завод, если выполняет заказ в срок; bi — неустойка, которую выплачивает завод в случае, если заказ не был выполнен к дню di включительно. Нумерация дней ведется со следующего после заключения договоров дня. Известно, что на выполнение одного заказа завод тратит непрерывный отрезок из ровно K дней, причем в один момент времени завод может быть занят только одним заказом.
В итоге перед директором по расписаниям стоит непростая задача: выбрать какие заказы выполнить (и в какое время), а за какие проще сразу заплатить неустойку.
Конкурирующая фирма хочет данное предприятие разорить. У директора конкурирующей фирмы есть возможность перехватить любое число заказов. Все остальные заказы достанутся предприятию (даже если они явно ему не выгодны). Требуется помочь директору конкурирующей фирмы выбрать такое подмножество имеющихся потенциальных заказов для перехвата, чтобы при оптимальной работе директора по расписаниям (то есть при выборе им наилучшей стратегии выполнения оставшихся заказов) доход предприятия был минимальным (он может быть и отрицательным).
В первой строке входного файла записано одно число G — номер группы тестов. Во второй строке задано два числа N и K. Следующие N строк содержат описание заказа: di, ai, bi. Числа K, ai, bi целые положительные и не превосходят 1 000. Числа di целые положительные и не превосходят 100 000.
В первой строке выведите значение искомого дохода (убытка) предприятия. Следующая строка должна содержать ровно N нулей и единиц, разделенных пробелами. Если на i-й позиции стоит 0, это означает, что этот заказ должна перехватить конкурирующая фирма; если же стоит 1, то заказ достанется предприятию.
1
4 1
1 9 9
1 4 4
1 3 3
1 3 3
-2
0 1 1 1
6
8 4
1 10 3
2 10 3
3 10 3
4 10 3
5 8 3
6 7 2
6 5 5
7 6 1
-10
1 1 1 1 1 1 1 1
Тесты состоят из девяти групп.
- Тесты 1–2, из условия, оцениваются в 0 баллов.
- В тестах этой группы 1 ≤ N ≤ 100 000, K = 1, di = 1, ai = bi для всех i. Эта группа оценивается в 10 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы 1 ≤ N ≤ 100 000, K = 1, di = 1 для всех i. Эта группа оценивается в 10 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы 1 ≤ N ≤ 100 000, ai = bi, di = dj, для всех i, j. То есть все заказы имеют одинаковый срок выполнения, и для всех заказов прибыль равна неустойке. Эта группа оценивается в 10 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы 1 ≤ N ≤ 1 000, di = dj, для всех i, j. Эта группа оценивается в 10 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы 1 ≤ N ≤ 100 000, di = dj, для всех i, j. Эта группа оценивается в 10 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы 1 ≤ N ≤ 15. Эта группа оценивается в 10 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы 1 ≤ N ≤ 100, ai = bi. На этой группе будут тестироваться только решения, прошедшие хотя бы одну из групп 1 - 6. Группа состоит из 20 тестов, за каждый тест участник получает либо 0, либо 1 балл. Участник получает за тест 1 балл, если его ответ корректен и никакое другое решение (другого участника или жюри) не находит ответ лучше.
- В тестах этой группы 1 ≤ N ≤ 100. На этой группе будут тестироваться только решения, прошедшие хотя бы одну из групп 1 - 6. Группа состоит из 20 тестов, за каждый тест участник получает либо 0, либо 1 балл. Участник получает за тест 1 балл, если его ответ корректен и никакое другое решение (другого участника или жюри) не находит ответ лучше.
В Москве происходит Важное Событие. Посмотреть на Важное Событие съехалось множество людей со всей страны. Во избежание давки и соблюдения порядка полицией была организована очередь, растянувшаяся по набережной Москвы-реки от станции метро X аж до станции метро Y!
Вся очередь разделена на N секторов с помощью перегородок с турникетами. Вход на Важное Cобытие расположен перед первой перегородкой, т.е. попасть туда можно только из сектора 1.
Раз в секунду через каждую перегородку, перед которой есть хотя бы один человек, в сторону События через турникет пропускают одного человека (то есть из сектора i в сектор i - 1, и из сектора 1 — на само Событие). Внутри сектора люди передвигаются существенно быстрее, поэтому этим временем можно пренебречь.
По известному количеству людей в секторах определите, через сколько секунд на Важное Событие попадет последний человек.
В первой строке заданы число секторов N и число непустых секторов M (1 ≤ N ≤ 109, 0 ≤ M ≤ 105). В следующих M строках записаны числа ai и bi — номер i-того непустого сектора и bi — количество человек в нем (1 ≤ a1 < a2 < ... < aM ≤ N, 1 ≤ bi ≤ 109)
Выведите одно целое число — время в секундах, через которое все люди смогут попасть на Важное Событие.
3 2
1 1
3 2
4
3 2
2 2
3 2
5
Тесты состоят из четырёх групп.
- Тесты 1–2, из условия, оцениваются в 0 баллов.
- В тестах этой группы N ≤ 1 000, и общее количество людей во всех секторах также не превосходит 1 000. Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы N ≤ 105, общее число людей тоже не превосходит 105. Эта группа оценивается в 30 баллов, они начисляются только при прохождении всех тестов группы.
- Баллы за тесты этой группы начисляются только при прохождении всех тестов 1-й и 2-й групп. Каждый тест оценивается независимо от других.
Вася участвовал в недавнем эксперименте: проведи 8 часов без гаджетов. Для того чтобы убить время, он стал проделывать со случайной строкой, состоящей только из нулей и единиц, следующую процедуру. Каждый ноль этой строки он заменял на строку S, тоже состоящую из нулей и единиц, а каждую единицу — на строку T, опять же из нулей и единиц. Строки S и T он выписал заранее. С полученной строкой он опять проделывал ту же самую процедуру, не меняя при этом строки S и T. За 8 часов он успел таким образом сделать K преобразований.
Помогите Васе определить, на каком по счету месте в итоговой строке окажется N-я единица, если гарантируется, что N единиц в этой строке есть. Нумерация символов в строке, как и подсчет единиц, ведется с единицы.
В первой строке входного файла находятся числа K (0 ≤ K ≤ 100 000) и N (1 ≤ N ≤ 1018). Во второй строке файла находится исходная строка. В третьей — строка S, в четвертой — строка T. Длина каждой из строк не превосходит 1 000 символов.
Выведите одно число — номер N-й единицы в итоговой строке. Гарантируется, что ответ не превосходит 1018.
1 3
01
10
11
4
3 10
0
101
01
17
Тесты состоят из пяти групп.
- Тесты 1–2, из условия, оцениваются в 0 баллов.
- В тестах этой группы 1 ≤ K ≤ 10, 1 ≤ N ≤ 10, длины строк во входном файле не превосходят 2. Баллы за тесты этой группы начисляются только при прохождении всех тестов 1-й группы. Эта группа оценивается в 20 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы 1 ≤ K ≤ 10, 1 ≤ N ≤ 106, гарантируется, что ответ не превосходит 106. Баллы за тесты этой группы начисляются только при прохождении всех тестов 2-й группы. Эта группа также оценивается в 20 баллов, они начисляются только при прохождении всех тестов группы.
- В тестах этой группы 1 ≤ K ≤ 1 000, 1 ≤ N ≤ 107, гарантируется, что ответ не превосходит 107. Баллы за тесты этой группы начисляются только при прохождении всех тестов 3-й группы. Эта группа также оценивается в 20 баллов, они начисляются только при прохождении всех тестов группы.
- Баллы за тесты этой группы начисляются только при прохождении всех тестов 4-й группы. Каждый тест оценивается независимо от других.
Напомним, что важнейшей задачей молекулярной биологии является изучение различных белков. В общем случае один и тот же белок имеет одну из четырех форм (первичная, вторичная, третичная и четвертичная структура), простейшей с точки зрения химии является первичная, которую мы и рассмотрим.
Белок представляет собой последовательность аминокислот, соединенных пептидной связью (эта связь одинакова между любыми двумя аминокислотами, поэтому рассматриваться она не будет). Аминокислота, как следует из названия, — это органическое соединение, в молекуле которого одновременно содержатся карбоксильные и аминные группы. Для простоты будем считать, что аминокислота состоит из химических элементов, каждый элемент будем обозначать маленькой латинской буквой, таким образом, аминокислота однозначно определяется строкой из нескольких латинских букв. Безусловно, не любая последовательность элементов является аминокислотой.
Для каждого организма известен большой список аминокислот, которые могут быть синтезированы в организме такого типа. Для удобства транскрипции (это один из этапов синтеза РНК), ни одна аминокислота не является началом другой.
Одна из часто встречающихся задач заключается в том, чтобы понять, мог ли данный белок быть синтезирован в данном организме (это позволяет понять по белку, где он был синтезирован: у человека, у гриба и пр.). Для этого нужно проверить, все ли аминокислоты, из которых он состоит, могли быть синтезированы. Однако, часто белок содержит лишние элементы (например, к белку из-за обилия атомов водорода очень часто присоединяются молекулы воды), поэтому задача сводится к изучению фрагментов этого белка. Проводят как отдельные проверки каких-то фрагментов, так и целые серии проверок случайных фрагментов.
Более формально, вам дан словарь из аминокислот, каждая из которых представляет собой строку из маленьких латинских букв, и белóк, который также представляет собой строку из маленьких латинских букв. Необходимо ответить на несколько вопросов вида «мог ли фрагмент белка с позиции l по r быть синтезирован из данных аминокислот», т. е. можно ли данный фрагмент разбить на слова из словаря. В случае положительного ответа, необходимо предъявить минимальное количество слов в таком разбиении.
В первой строке входного файла содержится одно число N — количество аминокислот. Далее следует N непустых строк, каждая из которых является описанием аминокислоты. Суммарная длина строк S не превосходит 106.
В следующей строке содержится исходный белок, длина L которого не превосходит 106.
Далее содержится число M — количество простых запросов (0 ≤ M ≤ 105). Каждый простой запрос описывается двумя числами — l и r, (1 ≤ l ≤ r ≤ L), обозначающими искомый фрагмент [l, r], который необходимо разбить.
Далее содержится число K — количество запросов-серий (0 ≤ K ≤ 105, в некоторых группах тестов запросы-серии отсутствуют и K = 0).
Каждая серия описывается восемью целыми числами T, A, B, C, D, E, l1, r1 (1 ≤ A, B, C, D ≤ 100,
1 ≤ T, E, l1, r1 ≤ 107). Такая серия описывает T простых запросов. Запрос с номером i выглядит как фрагмент 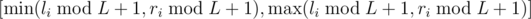 . Числа li и ri для i ≥ 2 определяются следующим образом. Пусть ans обозначает ответ на запрос с
номером i - 1 в этой серии. Тогда
. Числа li и ri для i ≥ 2 определяются следующим образом. Пусть ans обозначает ответ на запрос с
номером i - 1 в этой серии. Тогда 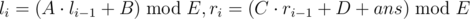 . Суммарное число запросов в сериях не превосходит
107.
. Суммарное число запросов в сериях не превосходит
107.
Все строки во входном файле состоят только из маленьких латинских букв. Гарантируется. что ни одна аминокислота не является префиксом другой.
Для каждого простого запроса выведите единственное число — минимальное число аминокислот, на которое разбивается соответсвующий фрагмент. В случае, если разбиения не существует, ответом на запрос является число - 1. Для каждой серии выведите одно число — сумму ответов на все запросы, для которых ответ существует (то есть не равен - 1), взятую по модулю E.
2
abra
cadabra
abracadabra
6
1 4
8 11
4 8
5 11
1 11
3 6
0
1
1
-1
1
2
-1
2
ab
ba
ababab
0
1
10 1 2 3 4 5 6 7
3
Тесты состоят из пяти групп.
- Тесты 1–2, из условия, оцениваются в 0 баллов.
- В тестах этой группы общая длина словарных аминокислот S не превосходит 5 000, длина белка L не превосходит 5 000, число простых запросов M не превосходит 5 000, запросы-серии отсутствуют (K = 0). Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы суммарная длина аминокислот S не превосходит 500 000, длина белка L не превосходит 5 000, число простых запросов M не превосходит 5 000, запросы-серии отсутствуют (K = 0). Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы суммарная длина аминокислот S не превосходит 500 000, длина белка L не превосходит 100 000, число простых запросов M не превосходит 100 000, запросы-серии отсутствуют (K = 0). Эта группа оценивается в 20 баллов, баллы начисляются только при прохождении всех тестов группы.
- Баллы за тесты этой группы начисляются только при прохождении всех тестов всех предыдущих групп. Некоторые тесты этой группы объединяются в подгруппы, тесты за каждую подгруппу ставятся только при прохождении всех тестов подгруппы.
В новой телевизионной игре участник должен попасть извне в центр системы вложенных крепостей. Каждая крепость представляет собой выпуклый многоугольник, крепости друг друга не касаются. Центральная точка имеет координаты (0, 0) и находится в самой внутренней крепости. Каждая крепость имеет несколько «дверей». Для каждой двери известно время, затрачиваемое на проход через нее. Проходить через крепостную стену вне дверей нельзя. Скорость передвижения участника вне дверей постоянна и равна 1, то есть время передвижения на расстояние S равно S.
Участник изначально находится в одной из дверей внешнего многоугольника (он сам может выбирать, в какой). Его цель — добраться до точки (0, 0) как можно быстрее. Но в игре существует следующее ограничение: когда участник вошел в какую-то дверь, в качестве следующей двери он может выбрать только такую, которая сейчас находится вне зоны его прямой видимости. Если игрок смотрит вдоль стены, то он видит находящиеся в ней двери.
Требуется определить, может ли участник добраться до финиша, и если да, то за какое минимальное время он может это сделать при оптимальном выборе стартовой двери.
В первой строке входного файла задано единственное число N (1 ≤ N ≤ 105) — количество крепостей. Далее идут N блоков данных в следующем формате: в первой строке блока содержится число K (3 ≤ K ≤ 105) — количество вершин многоугольника, описывающего крепостную стену. За ней следуют K строк, в каждой из которых записано два числа x, y — координаты соответствующей вершины. В следующей строке идет число M (1 ≤ M ≤ 105) — число дверей, расположенных на границе этого многоугольника. Затем идут M строк, каждая из которых содержит три числа x, y, t — координаты двери и время прохода через нее. Все координаты целые, по модулю не превосходящие 109. Время прохода t — целое число, 0 ≤ t ≤ 106. Общее количество вершин многоугольников, а также общее число дверей не превосходит 3·105. Гарантируется, что каждая дверь находится на границе или в вершине соответствующего многоугольника.
Первый блок соответствует внешнему многоугольнику (тому, с которого участник начинает игру), второй — вложенному в него, ..., последний блок соответствует самому внутреннему многоугольнику.
Вершины многоугольников заданы в порядке обхода против часовой стрелки. Никакие три последовательные вершины не лежат на одной прямой. Двери могут быть заданы в произвольном порядке.
Гарантируется, что при i = 1, 2, ..., N - 1 каждая точка i + 1-го многоугольника находится строго внутри i-го. Все многоугольники содержат точку (0, 0).
Выведите одно число — минимальное время, за которое участник может добраться до финиша, с абсолютной или относительной точностью 10 - 6. Если участник не может закончить игру, выведите одно число «-1» (без кавычек).
2
4
4 3
-3 3
-3 -2
4 -2
2
-3 0 3
-2 3 2
4
1 2
-1 2
-1 -1
1 -1
3
0 2 10
0 -1 4
-1 2 1
11.236067
Тесты состоят из пяти групп.
- Тест из условия, оценивается в 0 баллов.
- В тестах этой группы суммарное количество вершин и дверей не превосходит 100, а каждая крепостная стена описывается прямоугольником со сторонами, параллельными осям координат. Эта группа оценивается в 20 баллов, баллы начисляются только при прохождении всех тестов группы.
- В тестах этой группы суммарное количество вершин и дверей не превосходит 100. Баллы за тесты этой группы начисляются только при прохождении всех тестов 1-ой группы. Эта группа также оценивается в 20 баллов, они начисляются только при прохождении всех тестов группы.
- В тестах этой группы суммарное количество вершин не превосходит 2000, суммарное количество дверей не превосходит 2000. Баллы за тесты этой группы начисляются только при прохождении всех тестов 1-ой и 2-й групп. Эта группа также оценивается в 20 баллов, они начисляются только при прохождении всех тестов группы.
- Баллы за тесты этой группы начисляются только при прохождении всех тестов 1-ой, 2-ой и 3-ей групп. Каждый тест оценивается независимо от других.