Перебор с отсечением(22 задач)
Простые задачи на перебор(43 задач)
Гамильтонов цикл(2 задач)
Как много открытий можно сделать, исследуя числа и составляющие их цифры!
Петя очень любит арифметику, и кроме домашних заданий он постоянно придумывает дополнительные задачи. Однажды он стал прибавлять к натуральным числам сумму составляющих их цифр. Петя обнаружил, что некоторые числа, например 20, не могут быть получены из других чисел в результате такого действия. Эти числа ему не понравились, и он назвал их некрасивыми.
Позже, когда Петя начал изучать информатику, те же исследования он стал проводить с натуральными числами в двоичной системе счисления. Например, двоичное число 11102 (в десятичной системе — 14) можно получить из числа 11002 (в десятичной системе — 12), прибавив к последнему сумму его цифр:
11002 + 102 = 11102.
Петя решил исследовать множество двоичных некрасивых чисел. Первые пять некрасивых чисел он нашел без труда: 1 = 12, 4 = 1002, 6 = 1102, 13 = 11012, 15 = 11112. Продолжить работу он собирается с помощью компьютера.
Требуется написать программу, которая определяет количество двоичных некрасивых чисел, не превосходящих заданного числа n.
В первой строке входного файла содержится число n, записанное в десятичной системе счисления (1 ≤ n ≤ 1018).
В единственной строке выходного файла должно содержаться единственное число — количество двоичных некрасивых чисел, не превосходящих n.
Примечание
Решения, корректно работающие при n ≤ 106, будут оцениваться из 40 баллов.
17
5
18
6
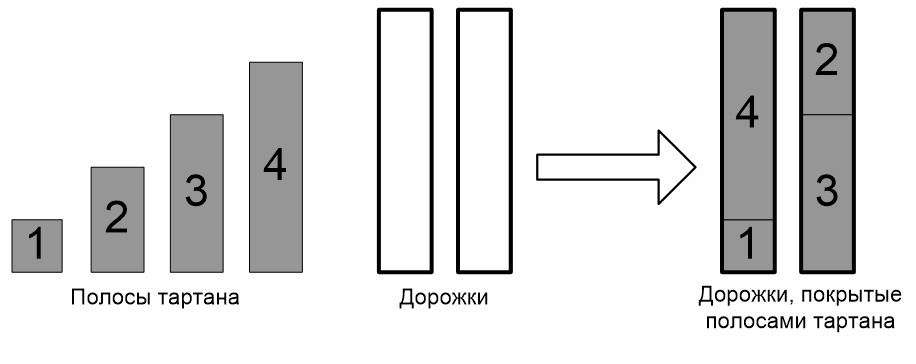
В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).
Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.
Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.
Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).
В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».
В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.
В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.
Примеры входных и выходных данных
| Ввод | Вывод |
| 2 4 | YES 2 1 4 2 3 2 |
| 3 4 | NO |