Перебор с отсечением(22 задач)
Простые задачи на перебор(43 задач)
Гамильтонов цикл(2 задач)
Обычно автобусный билет с номером, состоящим из 6 цифр, считается счастливым, если сумма первых трех цифр его номера была равна сумме трех последних. Школьник Вася очень любил получать счастливые билеты, однако это случалось не так часто. Поэтому для себя он изменил определение счастливого билета. Счастливым он считал тот номер, сумма некоторых цифр которого равнялась сумме оставшихся цифр. В его представлении билет с номером 561743 счастливый, так как 5 + 1 + 4 + 3 = 6 + 7.
Вася вырос, но по привычке в номерах различных документов пытается найти признаки счастливого номера ☺. Для этого он расширил свое определение счастливого номера на n-значные номера лицевых счетов и других документов, состоящих из цифр от 0 до k (1 ≤ k ≤ 9). Номер документа он называет счастливым, если сумма некоторых цифр этого номера равняется сумме оставшихся. Остальные номера для него несчастливые. К сожалению, несмотря на расширенное понимание “счастья”, несчастливых номеров остается еще много...
Вам предлагается определить количество несчастливых n-значных номеров, которые можно составить, используя цифры от 0 до k. В номерах допускается любое количество ведущих нулей.
Входной файл unlucky.in содержит описание нескольких видов номеров. Каждый вид номеров определяется значениями n и k. Для данного входного файла вы должны создать соответствующий ему выходной файл и отправить его на проверку жюри.
Входной файл содержит несколько пар значений n и k, каждая пара записана в отдельной строке.
Для каждой пары значений n и k входного файла выведите в соответствующей строке выходного файла искомое количество несчастливых билетов или 0, если такое число вам получить не удалось. Количество строк во входном и выходном файлах должно совпадать.
За правильное решение задачи для каждого вида номеров вы получите 5 баллов. Так, представленный в примере выходной файл соответствует 15 баллам.
При сдаче на проверку выходного файла во время тура вы будете получать одно из двух сообщений:
4 1 7 1 3 2 6 2 22 2 7 9 8 7 9 6 8 8 12 9 20 9 20 3 17 5 16 7 15 9 19 5 26 9 100 3 99 4 50 5
Как много открытий можно сделать, исследуя числа и составляющие их цифры!
Петя очень любит арифметику, и кроме домашних заданий он постоянно придумывает дополнительные задачи. Однажды он стал прибавлять к натуральным числам сумму составляющих их цифр. Петя обнаружил, что некоторые числа, например 20, не могут быть получены из других чисел в результате такого действия. Эти числа ему не понравились, и он назвал их некрасивыми.
Позже, когда Петя начал изучать информатику, те же исследования он стал проводить с натуральными числами в двоичной системе счисления. Например, двоичное число 11102 (в десятичной системе — 14) можно получить из числа 11002 (в десятичной системе — 12), прибавив к последнему сумму его цифр:
11002 + 102 = 11102.
Петя решил исследовать множество двоичных некрасивых чисел. Первые пять некрасивых чисел он нашел без труда: 1 = 12, 4 = 1002, 6 = 1102, 13 = 11012, 15 = 11112. Продолжить работу он собирается с помощью компьютера.
Требуется написать программу, которая определяет количество двоичных некрасивых чисел, не превосходящих заданного числа n.
В первой строке входного файла содержится число n, записанное в десятичной системе счисления (1 ≤ n ≤ 1018).
В единственной строке выходного файла должно содержаться единственное число — количество двоичных некрасивых чисел, не превосходящих n.
Примечание
Решения, корректно работающие при n ≤ 106, будут оцениваться из 40 баллов.
17
5
18
6
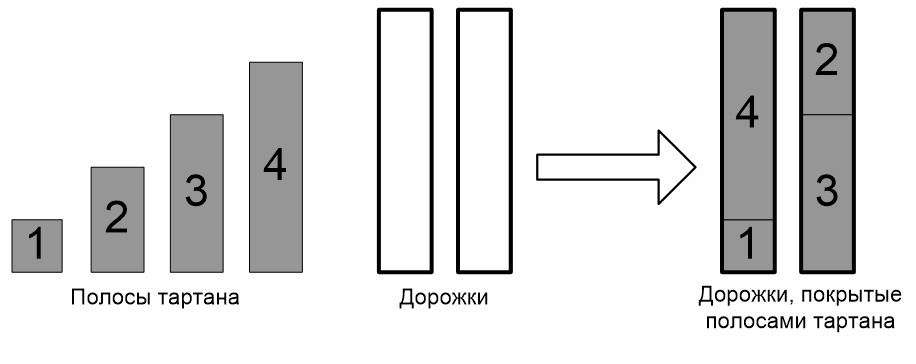
В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).
Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.
Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.
Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).
В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».
В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.
В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.
Примеры входных и выходных данных
| Ввод | Вывод |
| 2 4 | YES 2 1 4 2 3 2 |
| 3 4 | NO |
Cреди всех прямоугольных параллелепипедов с натуральными длинами сторон и площадью поверхности не более \(n\) найти тот, объём которого максимален.
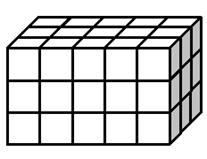
Начинающий программист Поликарп очень любит дарить подарки, особенно в коробках. Он давно заметил, что если коробка красиво оформлена, то радость от подарка возрастает многократно. Любой обёрточной бумаге он предпочитает клетчатую. В самом деле, после распаковки подарка на ней можно играть в крестики-нолики, морской бой, точки, а также решать задачи и писать программы.
Поликарп очень аккуратен. Он упаковывает подарок в коробку, имеющую форму прямоугольного параллелепипеда, и оклеивает всю её поверхность клетчатой бумагой. При этом каждая грань коробки представляет собой прямоугольник, состоящий из целых клеток. На рисунке изображён пример такой упаковки подарка.
В настоящий момент Поликарп собирается поздравить свою подругу, недавно вернувшуюся с очередной олимпиады. Он хочет подарить ей подарок в большой и красивой коробке.
У Поликарпа в наличии есть лист клетчатой бумаги, состоящий из \(n\) клеток. Каким будет максимальный объём коробки, которую можно оклеить с использованием этого листа бумаги описанным выше способом? Поликарп может разрезать лист клетчатой бумаги по границам клеток произвольным образом и оклеивать коробку получившимися фигурами, поэтому форма листа не важна, а имеет значение только количество клеток на нём. Поликарп может использовать для оклеивания коробки не все клетки.
Напишите программу, которая по заданному количеству клеток \(n\) находит размеры коробки максимального возможного объема.
Входной файл содержит одно целое число \(n\) (\(6\le n\le10^{13}\)) — количество клеток на листе клетчатой бумаги.
Выведите в первую строку выходного файла максимальный объём коробки, которую может подарить Поликарп. Объём следует выводить в «кубических клетках», то есть единицей измерения является куб со стороной, равной длине стороны клетки.
Во вторую строку выведите ширину, длину и высоту искомой коробки. Единица измерения — размер клетки. Числа разделяйте пробелами. Если решений несколько, то выведите любое из них.
Система оценивания
Решения, корректно работающие при \(n\le5\,000\), будут оцениваться из 30 баллов, а решения, корректно работающие при \(n\le10^8\), будут оцениваться из 70 баллов.
6
1 1 1 1
24
8 2 2 2
Задано множество из \(n\) станций и \(m\) трубопроводов, соединяющих некоторые пары станций. Требуется выбрать множество из \(k\) станций, чтобы один из двух концов каждого трубопровода лежал в выбранном множестве. Если построить граф, в котором станции будут служить вершинами, а трубопроводы — рёбрами, то искомое множество будет являться вершинным покрытием в этом графе.
Ханты-Мансийский автономный округ — Югра является важнейшим нефтяным регионом России. Добыча нефти составляет 267 млн т в год, её транспортировка осуществляется по трубопроводам, общая длина которых превышает длину экватора Земли.
Система транспортировки нефти представляет собой совокупность \(n\) распределительных станций и \(m\) трубопроводов. Каждый трубопровод соединяет две различные станции. Между любыми двумя станциями проложено не более одного трубопровода.
Эффективность работы станций существенно зависит от вязкости нефти. Поэтому компания «ЮграНефтеТранс», в ведении которой находится сеть трубопроводов, заказала инновационному исследовательскому предприятию разработку и изготовление новых сверхточных датчиков вязкости на основе самых современных технологий.
Изготовление датчиков — процесс трудоёмкий и дорогостоящий, поэтому было решено изготовить \(k\) датчиков (\(k\le40\)) и выбрать \(k\) различных станций, на которых датчики будут установлены. Необходимо осуществить выбор станций так, чтобы датчики контролировали все трубопроводы: для каждого трубопровода хотя бы один датчик должен быть установлен на станции, где начинается или заканчивается этот трубопровод.
Напишите программу, которая проверяет, существует ли требуемое расположение датчиков, и в случае положительного ответа находит это расположение.
В первой строке входного файла записаны три натуральных числа — \(n\), \(m\) и \(k\) (\(k\le n\le2000\), \(1\le m\le10^5\), \(1\le k\le40\)). Далее следуют \(m\) строк, каждая из которых описывает один трубопровод. Трубопровод задаётся двумя целыми числами — порядковыми номерами станций, которые он соединяет. Станции пронумерованы от 1 до \(n\). Гарантируется, что к любой станции подведён хотя бы один трубопровод и между любыми двумя станциями проложено не более одного трубопровода. Числа в каждой строке разделены пробелами.
В первую строку выходного файла выведите слово «Yes», если требуемое расположение датчиков существует, в противном случае — слово «No». В случае положительного ответа выведите во вторую строку выходного файла \(k\) различных целых чисел — номера станций, на которых необходимо установить датчики. Номера можно выводить в любом порядке. Если существует несколько подходящих расположений датчиков, выведите любое из них. Разделяйте числа во второй строке пробелами.
Система оценивания
Решения, корректно работающие при \(n\le100\) и \(k\le10\), будут оцениваться из 60 баллов.
9 12 4 1 2 2 3 1 4 4 5 1 6 6 7 1 8 8 9 2 5 4 7 6 9 8 3
Yes 2 4 6 8
8 12 4 7 4 7 5 3 1 2 8 4 3 3 2 6 1 1 2 1 4 6 5 8 6 8 7
No
4 3 1 3 1 3 2 3 4
Yes 3