Страница: << 1 2 Отображать по:
#3398
Велогонка
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Велосипедисты, участвующие в шоссейной гонке, в некоторый момент времени, который называется начальным, оказались в точках, удалённых от места старта на \(x_1\), \(x_2\), ..., \(x_n\) метров (\(n\) – общее количество велосипедистов). Каждый велосипедист двигается со своей постоянной скоростью \(v_1\), \(v_2\), ..., \(v_n\) метров в секунду. Все велосипедисты двигаются в одну и ту же сторону.

Репортёр, освещающий ход соревнований, хочет определить момент времени, в который расстояние между лидирующим в гонке велосипедистом и замыкающим гонку велосипедистом станет минимальным, чтобы с вертолёта сфотографировать сразу всех участников велогонки.

Требуется написать программу, которая по заданному количеству велосипедистов \(n\), заданным начальным положениям велосипедистов \(x_1\), \(x_2\), ..., \(x_n\) и их скоростям \(v_1\), \(v_2\), ..., \(v_n\), вычислит момент времени \(t\), в который расстояние \(l\) между лидирующим и замыкающим велосипедистом будет минимальным.

Входные данные

Первая строка входного файла содержит целое число \(n\) – количество велосипедистов.

В последующих n строках указаны по два целых числа: \(x_i\) – расстояние от старта до \(i\)-го велосипедиста в начальный момент времени (\(0 \leq x_i \leq 10^7\)) и \(v_i\) – его скорость (\(0 \leq v_i \leq 10^7\)).

Выходные данные

В выходной файл необходимо вывести два вещественных числа: \(t\) – время в секундах, прошедшее от начального момента времени до момента, когда расстояние в метрах между лидером и замыкающим будет минимальным, \(l\) – искомое расстояние.

Числа t и l должны иметь абсолютную или относительную погрешность не более \(10^{–6}\), что означает следующее. Пусть выведенное число равно \(x\), а в правильном ответе оно равно \(y\). Ответ будет считаться правильным, если значение выражения \(|x – y| / max(1, |y|)\) не превышает \(10^{–6}\).

Подзадачи и система оценки

Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 1 (20 баллов)

\(2 \leq n \leq 50\), \(0 \leq  x_i \leq 1000\), \(0 \leq v_i \leq 1000\). Гарантируется, что существует ответ, в котором \(t\) – целое число, не превышающее 1000.

Подзадача 2 (20 баллов)

\(2 \leq n \leq 200\).

Подзадача 3 (30 баллов)

\(2 \leq n \leq 2000\)

Подзадача 4 (30 баллов)

\(2 \leq n \leq 10^5\)

Примеры
Входные данные
3
0 40
30 10
40 30
Выходные данные
1 30
Входные данные
5
90 100
100 70
100 70
110 60
120 35
Выходные данные
0.5 5.000000000000
#3399
Сад пермского периода
  
ограничение по времени на тест
1.5 second;
ограничение по памяти на тест
256 megabytes

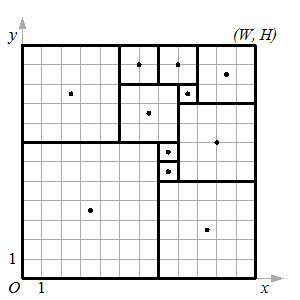
Оранжерея “Сад пермского периода” представляет собой прямоугольный участок для выращивания растений пермского периода. Оранжерея была разбита дорожками на квадраты. В центре каждого квадрата посажено одно растение. Размер квадрата зависит от корневой системы растения.

За год дорожки заросли травой, что затруднило уход за оранжереей. Чтобы при садовых работах не повредить корневую систему какого-либо растения, по имеющемуся расположению растений необходимо восстановить размеры соответствующих им квадратов.

Введем декартову прямоугольную систему координат, начало которой совмещено с левым нижним углом оранжереи. Ось \(Ox\) направлена вдоль нижней границы участка, ось \(Oy\) – вдоль левой. Изначально дорожки были проложены параллельно осям координат. Единичный отрезок удалось выбрать так, что координаты углов каждого из квадратов оказались целыми.

Требуется написать программу, которая по размеру оранжереи и координатам растений определит размеры соответствующих им квадратов.

Входные данные

В первой строке входного файла записаны три натуральных числа: \(W\) – ширина оранжереи, \(H\) – длина оранжереи и \(N\) – количество посаженых растений. В каждой из следующих \(N\) строк расположены по два числа: \(x_i\), \(y_i\) – координаты \(i\)-го растения (\(0 \lt x_i \lt W\), \(0 \lt y_i \lt H\)). Гарантируется, что соответствующие растениям квадраты имеют целую длину стороны и покрывают всю оранжерею.

Выходные данные

В выходной файл необходимо вывести \(N\) целых чисел – размеры квадратов, соответствующих растениям. Числа требуется вывести в порядке описания растений во входном файле.

Комментарий

Оранжерея во втором примере соответствует следующему рисунку:

Подзадачи и система оценки

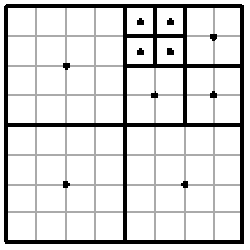
Данная задача содержит пять подзадач. Следующая группа тестируется только при прохождении предыдущей.

Подзадача 1 (10 баллов)

\(W = H \leq 10\); \(N \leq 6\). Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 2 (20 баллов)

\(W, H \leq 20\); \(N \leq 20\). Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 3 (30 баллов)

\(W, H \leq 1000\); \(N \leq 1000\). Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 4 (20 баллов)

\(W, H \leq 2\times 10^5\); \(N \leq 2\times 10^5\). Каждый тест для данной подзадачи оценивается отдельно.

Подзадача 5 (20 баллов)

\(W, H \leq 2\times 10^{12}\); \(N \leq 2\times 10^5\). Каждый тест для данной подзадачи оценивается отдельно.

Примеры
Входные данные
4 6 3
1 1
3 1
2 4
Выходные данные
2
2
4
Входные данные
8 8 10
4.5 7.5
5.5 7.5
2 6
4.5 6.5
7 7
5 5
6 2
7 5
2 2
5.5 6.5
Выходные данные
1
1
4
1
2
2
4
2
4
1
#3400
Распил бревен
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Лесопильный комбинат выполняет заказ на распил брусьев для строительства детского городка. Все готовые брусья должны иметь форму треугольных призм, основаниями которых являются равнобедренные треугольники. Для изготовления брусьев закуплены заготовки в виде половинок продольно распиленных бревен. Заготовки не являются идеальными половинками цилиндров, поэтому при изготовлении бруса необходимо учитывать форму заготовок. Комбинат заинтересован в изготовлении бруса с наибольшей возможной площадью поперечного сечения.

Для каждой заготовки измеряется несколько сечений. Каждое из них задано в виде ломаной, представленной координатами ее вершин (\(x_0, y_0\)), (\(x_1, y_1\)), ..., (\(x_N, y_N\)) в порядке их следования. Координаты вершин ломанной удовлетворяют следующим условиям:

\(x_0 < x_1 < x_2 < \dots < x_N\);

\(x_i = 0\) для некоторого \(0 < i < N\);

\(y_0 = y_N = 0\);

\(y_0 = y_N = 0\);

для всех \(i\) от 1 до (\(N – 1\)) выполнено условие \(y_i > 0\).

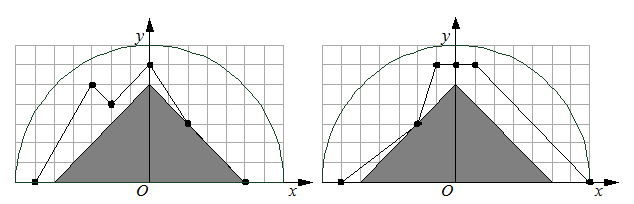
С учетом описанных требований необходимо найти максимально возможную площадь равнобедренного треугольника, удовлетворяющего следующим условиям:

основание треугольника лежит на оси абсцисс;

основание симметрично относительно начала координат;

треугольник полностью лежит внутри каждого из измеренных сечений заготовки.

Требуется написать программу, которая по заданным сечениям заготовки вычислит максимально возможную площадь искомого равнобедренного треугольника.

Входные данные

Первая строка входного файла содержит целое число \(K\) – количество измеренных сечений.

Далее следуют описания каждого из \(K\) сечений. В первой строке описания сечения содержится число \(N_K\) – количество звеньев ломаной. За ней следуют (\(N_K + 1\)) строк, каждая из которых содержит пару целых чисел \(x_i\) и \(y_i\) – координаты вершин ломаной сечения в порядке их следования.

Выходные данные

Выходной файл должен содержать одно вещественное число – наибольшую возможную площадь треугольника. Эта площадь должна иметь абсолютную или относительную погрешность не более \(10^{–6}\), что означает следующее. Пусть выведенное число равно \(x\), а в правильном ответе оно равно \(y\). Ответ будет считаться правильным, если значение выражения \(|x – y| / max(1, |y|)\) не превышает \(10^{–6}\).

Подзадачи и система оценки

Данная задача содержит пять подзадач.

Подзадача 1 (20 баллов)

\(K = 1\), \(N_1 \leq 15\), координаты вершин по модулю не превышают 20.

Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 2 (10 баллов)

\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.

Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 3 (20 баллов)

\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\).

Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 4 (10 баллов)

\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.

Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Подзадача 5 (40 баллов)

\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\).

Каждый тест для данной подзадачи оценивается отдельно.

Примеры
Входные данные
2
5
-6 0
-3 5
-2 4
0 6
2 3
5 0
5
-6 0
-2 3
-1 6
0 6
1 6
7 0
Выходные данные
25.0
Страница: << 1 2 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест