Возвращаясь из школы домой, Петя каждый раз обращал внимание на надпись на заборе «1 + 1 = 10» и удивлялся очевидной его неправоте. Но однажды его осенило, что это равенство верное, если рассматривать его в двоичной системе счисления. Его настолько поразила эта идея, что он решил непременно придумать свои три числа так, чтобы сумма первых двух была равна третьему в некоторой системе счисления.

Теперь он перебирает тройки чисел, которые, на его взгляд, достойны находиться на заборе. Петя выбирает числа A, B, C, записывающиеся десятичными цифрами, и дальше пытается найти основание системы счисления K, в которой равенство A + B = C оказалось бы верным. Петя рассматривает системы счисления с основанием от 2 до бесконечности.

Поскольку проверка каждой тройки — занятие трудоемкое, в помощь Пете необходимо написать программу, облегчающую расчеты.

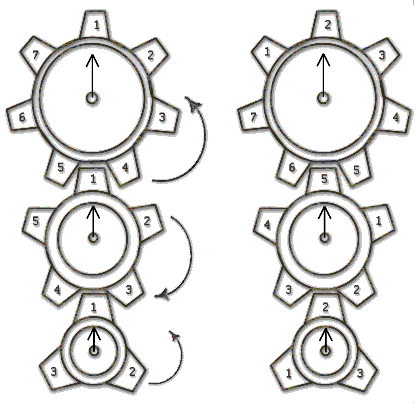На каждой из трех осей установлено по одной вращающейся шестеренке и неподвижной стрелке. Шестеренки соединены последовательно. На первой шестеренке n зубцов, на второй — m, на третьей — k. На каждом зубце первой, второй и третьей шестеренок по часовой стрелке написаны в порядке возрастания числа от 1 до n, от 1 до m и от 1 до k соответственно. Стрелки зафиксировали таким образом, что когда стрелка первой оси указывает на число, стрелки двух других осей также указывают на числа. Витя записывает три числа (a₁,a₂,a₃), на которые указывают стрелки. После этого он поворачивает первую шестеренку на угол 360°/n против часовой стрелки, чтобы напротив стрелки на первой оси оказался следующий (по часовой стрелке) зубец. При этом вторая шестеренка поворачивается на угол 360°/m по часовой стрелке (размеры зубцов у шестеренок одинаковые, поэтому размеры самих шестеренок разные, чтобы на границе шестеренок равномерно уложилось разное число одинаковых по размеру зубцов), а третья шестеренка поворачивается на угол 360°/k против часовой стрелки. Витя опять записывает три числа, на которые указывают стрелки.

Поступая и далее таким образом, Витя заметил, что после некоторого количества таких действий стрелки показывают на три первоначальных числа.

Теперь его очень интересует, как по двум данным тройкам чисел определить, принадлежат ли они к одной последовательности, то есть можно ли некоторым количеством поворотов перейти от первой тройки ко второй. Он попросил вас написать программу, которая отвечает на этот вопрос.

В настольном теннисе в результате каждой подачи разыгрывается одно очко. Подача переходит от игрока к игроку каждые 5 подач, т.е. первые пять раз подает первый игрок, затем 5 раз — второй, затем снова первый и т.д.

Партия играется до тех пор, пока кто-нибудь из игроков не наберет 21 очко. Тот, кто набрал 21 очко, признается победителем, и игра заканчивается.

Вася и Петя играли в игру, и забыли, кто должен подавать в данный момент. Однако они помнят, что первую подачу делал Вася, и счет в настоящий момент a:b (a очков у Васи и b очков у Пети). Напишите программу, которая по данным a и b будет определять, чья подача или устанавливать, что игра закончена.

Вася, решая задачи демо-версии ЕГЭ, дошел до задачи B5, которая звучит так.

«У исполнителя Калькулятор две команды:

· прибавь 3

· умножь на 4

Выполняя первую из них, Калькулятор прибавляет к числу на экране 3, а выполняя вторую, умножает его на 4.»

Далее в задаче требовалось получить из числа 3 число 57 не более, чем за 6 команд. Однако Вася заинтересовался, как можно для произвольных чисел \(a\) и \(b\) построить программу наименьшей длины получения числа \(b\) из числа \(a\).

Напишите программу, которая по заданным числам \(a\) и \(b\) вычислит наименьшее количество команд Калькулятора, которое нужно, чтобы получить из \(a\) число \(b\).