Таймер - это часы, которые умеют подавать звуковой сигнал по прошествии некоторого периода времени. Напишите программу, которая определяет, когда должен быть подан звуковой сигнал.

Одна из команд-участниц олимпиады решила вернуться домой на электричках. При этом ребята хотят попасть домой как можно раньше. К сожалению, не все электрички идут от города, где проводится олимпиада, до станции, на которой живут ребята. И, что еще более обидно, не все электрички, которые идут мимо их станции, останавливаются на ней (равно как вообще, электрички останавливаются далеко не на всех станциях, мимо которых они идут)

Все станции на линии пронумерованы числами от 1 до N. При этом станция номер 1 находится в городе, где проводится олимпиада, и в момент времени 0 ребята приходят на станцию. Станция, на которую нужно попасть ребятам, имеет номер E.

Напишите программу, которая по данному расписанию движения электричек вычисляет минимальное время, когда ребята могут оказаться дома.

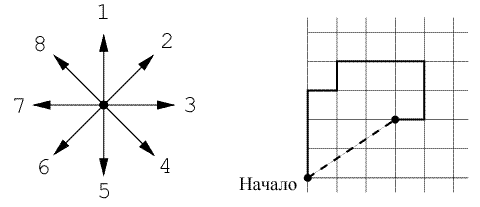
Найти закопанный пиратами клад просто: всё, что для этого нужно – это карта. Как известно, пираты обычно рисуют карты от руки и описывают алгоритм нахождения клада так: «Встаньте около одинокой пальмы. Пройдите тридцать шагов в сторону леса, потом семнадцать шагов в сторону озера, …, наконец десять шагов в сторону большого булыжника. Клад находится под ним». Большая часть таких указаний просто сводится к прохождению какого-то количества шагов в одном из восьми направлений (1 – север, 2 – северо-восток, 3 – восток, 4 – юго-восток, 5 – юг, 6 – юго-запад, 7 – запад, 8 – северо-запад) (см. рис). Длина шага в любом направлении равна 1.

Путешествие по такому пути обычно является прекрасным способом посмотреть окрестности, однако в наше время постоянной спешки ни у кого нет времени на это. Поэтому кладоискатели хотят идти напрямую в точку, где зарыт клад. Например, вместо того, чтобы проходить три шага на север, один шаг на восток, один шаг на север, три шага на восток, два шага на юг и один шаг на запад, можно пройти напрямую, использовав около 3.6 шага (см. рис).

Вам необходимо написать программу, которая по указаниям пиратов определяет точку, где зарыт клад.

Легендарный учитель математики Юрий Петрович придумал забавную игру с числами. А именно, взяв произвольное целое число, он переводит его в двоичную систему счисления, получая некоторую последовательность из нулей и единиц, начинающуюся с единицы. (Например, десятичное число \(19=1\times2^4+0\times2^3+0\times2^2+1\times2^1+1\times2^0\) в двоичной системе запишется как \(10011_2\)). Затем учитель начинает сдвигать цифры полученного двоичного числа по циклу (так, что последняя цифра становится первой, а все остальные сдвигаются на одну позицию вправо), выписывая образующиеся при этом последовательности из нулей и единиц в столбик — он подметил, что независимо от выбора исходного числа получающиеся последовательности начинают с некоторого момента повторяться. И, наконец, Юрий Петрович отыскивает максимальное из выписанных чисел и переводит его обратно в десятичную систему счисления, считая это число результатом проделанных манипуляций. Так, для числа 19 список последовательностей будет таким:

10011

11001

11100

01110

00111

10011

…

и результатом игры, следовательно, окажется число \(1\times2^4+1\times2^3+1\times2^2+0\times2^1+0\times2^0=28\).

Поскольку придуманная игра с числами все больше занимает воображение учителя, отвлекая тем самым его от работы с ну очень одаренными школьниками, Вас просят написать программу, которая бы помогла Юрию Петровичу получать результат игры без утомительных ручных вычислений.