Алгоритмы(1657 задач)
Структуры данных(279 задач)
Интерактивные задачи(17 задач)
Другое(54 задач)
Для того чтобы проверить, как её ученики умеют считать, Мария Ивановна каждый год задаёт им на дом одну и ту же задачу – для заданного натурального A найти минимальное натуральное N такое, что N в степени N (N, умноженное на себя N раз) делится на A. От года к году и от ученика к ученику меняется только число A.
Вы решили помочь будущим поколениям. Для этого вам необходимо написать программу, решающую эту задачу.
Во входном файле содержится единственное число A (1 ≤ A ≤ \(10^9\) – на всякий случай; вдруг Мария Ивановна задаст большое число, чтобы «завалить» кого-нибудь…).
В выходной файл вывести единственное число N.
1
1
8
4
Вы являетесь одним из разработчиков новой компьютерной игры. Игра происходит на прямоугольной доске, состоящей из W×H клеток. Каждая клетка может либо содержать, либо не содержать фишку (см. рисунок).
Важной частью игры является проверка того, соединены ли две фишки путем, удовлетворяющим следующим свойствам:
При этом часть пути может оказаться вне доски. Например:
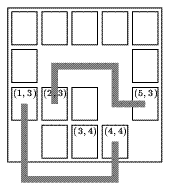
Фишки с координатами (1,3) и (4,4) могут быть соединены. Фишки с координатами (2,3) и (5,3) тоже могут быть соединены. А вот фишки с координатами (2,3) и (3,4) соединить нельзя – любой соединяющий их путь пересекает другие фишки.
Вам необходимо написать программу, проверяющую, можно ли соединить две фишки путем, обладающим вышеуказанными свойствами, и, в случае положительного ответа, определяющую минимальную длину такого пути (считается, что путь имеет изломы, начало и конец только в центрах клеток (или «мнимых клеток», расположенных вне доски), а отрезок, соединяющий центры двух соседних клеток, имеет длину 1).
Первая строка входного файла содержит два натуральных числа: W – ширина доски, H – высота доски (1≤W,H≤75). Следующие H строк содержат описание доски: каждая строка состоит ровно из W символов: символ «X» (заглавная английская буква «экс») обозначает фишку, символ «.» (точка) обозначает пустое место. Все остальные строки содержат описания запросов: каждый запрос состоит из четырёх натуральных чисел, разделённых пробелами – X1, Y1, X2, Y2, причём 1≤X1,X2≤W, 1≤Y1,Y2≤H. Здесь (X1, Y1) и (X2, Y2) – координаты фишек, которые требуется соединить (левая верхняя клетка имеет координаты (1,1)). Гарантируется, что эти координаты не будут совпадать (кроме последнего запроса; см. далее). Последняя строка содержит запрос, состоящий из четырёх чисел 0; этот запрос обрабатывать не надо. Количество запросов не превосходит 20.
Для каждого запроса необходимо вывести одно целое число на отдельной строке – длину кратчайшего пути, или 0, если такого пути не существует.
5 4 XXXXX X...X XXX.X .XXX. 2 3 5 3 1 3 4 4 2 3 3 4 0 0 0 0
5 6 0
4 4 XXXX XXXX XXXX XXXX 1 1 2 1 2 2 3 2 1 1 3 1 3 4 4 3 2 1 2 4 1 1 2 2 0 0 0 0
1 1 4 6 11 0
Во время недавних раскопок на Марсе были обнаружены листы бумаги с таинственными символами на них. После долгих исследований учёные пришли к выводу, что надписи на них на самом деле могли быть обычными числовыми равенствами. Если бы этот вывод оказался верным, это доказало бы не только то, что на Марсе много лет назад были разумные существа, но и то, что они уже умели считать…
Ученые смогли понять, что в этом случае означают найденные символы, и перевели эти равенства на обычный язык – язык цифр, скобок, знаков арифметических действий и равенства. Кроме того, из других источников было получено веское доказательство того, что марсиане знали только три операции – сложение, умножение и вычитание (марсиане никогда не использовали «унарный минус»: вместо «-5» они писали «0-5»). Также ученые доказали, что марсиане не наделяли операции разным приоритетом, а просто вычисляли выражения (если в них не было скобок) слева направо: например, 3+3*5 у них равнялось 30, а не 18.
К сожалению, символы арифметических действий марсиане почему-то наносили специальными чернилами, которые, как оказалось, были не очень стойкими, и поэтому в найденных листках между числами вместо знаков действий были пробелы. Если вся вышеизложенная теория верна, то вместо этих пробелов можно поставить знаки сложения, вычитания и умножения так, чтобы равенства стали верными. Например, если был найден лист бумаги с надписью «18=7 (5 3) 2», то возможна такая расстановка знаков: «18=7+(5-3)*2» (помните про то, в каком порядке марсиане вычисляют выражения!). В то же время, если попался лист с надписью «5=3 3», то марсиане явно не имели в виду числового равенства, когда писали это…
Вы должны написать программу, находящую требуемую расстановку знаков или сообщающую, что таковой не существует.
Первая строка входного файла состоит из натурального (целого положительного) числа, не превосходящего 230, знака равенства, и последовательности натуральных чисел (не более десяти), произведение которых также не превосходит 230. Некоторые группы чисел (одно или более) могут быть окружены скобками. Длина входной строки не будет превосходить 80 символов, и других ограничений на количество и вложенность скобок нет. Между двумя соседними числами, не разделенными скобками, всегда будет хотя бы один пробел, во всех остальных местах может быть любое (в том числе и 0) число пробелов (естественно, внутри числа пробелов нет).
В выходной файл необходимо вывести одну строку, содержащую полученное равенство (т.е., исходное равенство со вставленными знаками арифметических действий). В случае если требуемая расстановка знаков невозможна, вывести строку, состоящую из единственного числа \(-1\). Выходная строка не должна содержать пробелов.
Пример ответа для первого теста (ответ 1 - неправильный): 18=7+(5-3)*2
Пример ответа для второго теста (ответ 0 - неправильный): -1
18 = 7 (5 3) 2
1
5 = 3 3
0
В тридесятом государстве есть N деревень. Некоторые пары деревень соединены дорогами. В целях экономии, «лишних» дорог нет, т.е. из любой деревни в любую можно добраться по дорогам единственным образом.
Новейшие исследования показали, что тридесятое государство находится в сейсмически опасной зоне. Поэтому глава государства захотел узнать, какой именно ущерб может принести его державе землетрясение. А именно, он хочет узнать, какое минимальное число дорог должно быть разрушено, чтобы образовалась изолированная от остальных группа ровно изP деревень такая, что из любой деревни из этой группы до любой другой деревни из этой группы по-прежнему можно будет добраться по неразрушенным дорогам (группа изолирована от остальных, если никакая неразрушенная дорога не соединяет деревню из этой группы с деревней не из этой группы).
Вы должны написать программу, помогающую ему в этом.
Первая строка входного файла содержит два числа: N и P (1≤P≤N≤150). Все остальные строки содержат описания дорог, по одному на строке: описание дороги состоит из двух номеров деревень (от 1 до N), которые эта дорога соединяет. Все числа во входном файле разделены пробелами и/или переводами строки.
В выходной файл выведите единственное число – искомое количество дорог.
11 6 1 2 1 3 1 4 1 5 2 6 2 7 2 8 4 9 4 10 4 11
2