Страница: 1 Отображать по:

#111455

Щит

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Сыктывкар, 7-9 классы, 2013, Задача C ]

МОЗГ организация авторитетная. Ей поручают очень важные разработки. В данный момент многие из планетарных союзов в галактике заказывают разработку сторожевого силового щита вокруг их планет. И первой задачей при постройке такого щита является заказ ультраплотной плазмы. Ультраплазма невероятно дорога, поэтому заказывать с запасом — дорогого стоит.

Представим себе планеты как окружности с некоторым одинаковым радиусом, тогда щит нужно построить так:

$\text{[math]}$

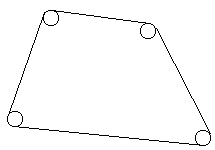
Вам дано количество планет в союзе, радиус для всех планет. Необходимо определить длину сечения сторожевого щита, это поможет оформить заказ на плазму с минимальными тратами.

Формат входного файла

В первой строке находятся два числа — количество гвоздей $N$, $1 \leq N \leq $100, и вещественное число $R$ — радиус планет.

Далее на входе располагаются еще $N$ строк, в каждой из которых записана через пробел пара вещественных координат очередной планеты; координаты не превосходят по абсолютной величине числа 100. Описания планет приводятся в порядке обхода вершин многоугольника (либо по часовой стрелке, либо против часовой стрелки), начиная с произвольного.

Формат выходного файла

Выведите вещественное число, округлённое до двух знаков после запятой — длину сечения щита.

Примеры

Входные данные

4 1
0.0 0.0
2.0 0.0
2.0 2.0
0.0 2.0

Выходные данные

14.28

#111456

Экстрасенсорика

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Сыктывкар, 7-9 классы, 2013, Задача D ]

Ученые из МОЗГ очень интересуются возможностями одноименного органа. Они очень близки к прорыву. Один из добровольцев уже в течении недели принимает препарат, которые позволяет ему читать мысли другого человека. И сегодня первый день серьезных испытаний.

Компьютер выдаст на монитор одному из участников проекта до $10^5$ целых чисел, которые нужно прочесть про себя. В этот же момент доброволец будет пытаться считать эти числа у первого из головы, а потом записать до $10^3$ чисел, которые запомнил.

Вам необходимо узнать результаты теста, чтобы продолжать испытания. Необходимо ответить на вопрос, сколько чисел из начального набора угадал испытуемый.

Формат входного файла

В первой строке целые числа $N$ ($1 \leq N \leq 10^5$) и $M$ ($1 \leq M \leq 10^3$) — количество исходных и угаданных чисел соответственно.

Во второй строке $N$ чисел — исходный набор различных, отсортированный в порядке возрастания.

В третьей строке $M$ чисел — предположения добровольца о числах.

Формат выходного файла

Выведите количество угаданных чисел.

Примеры

Входные данные

10 5
1 2 3 4 5 6 7 8 9 10
3 1 5 11 7

Выходные данные

Входные данные

10 10
1 2 3 4 5 11 12 13 14 15
20 21 22 23 24 25 26 27 28 29

Выходные данные

#111458

Палиндром

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Сыктывкар, 7-9 классы, 2013, Задача B ]

На одной из идеально круглых планет нашей галактики аборигены гордятся своей симметричностью и придерживаются ее во всем. Словарь «круглян» состоит исключительно из «симметричных» слов — палиндромов. Палиндром — слово, которое читается одинаково слева-направо и справа-налево, например топот, ротор. МОЗГ хочет наладить отношения с этой планетой, а для этого некоторые слова английского языка нужно привести к симметричному виду.

Вам будет дана строка из заглавных латинских букв. Необходимо дополнить ее справа минимальным количеством букв так, чтобы строка превратилась в палиндром, и вывести результат.

Формат входного файла

В единственной строке дана строка $S$, длиной до 200 символов из заглавных латинских букв.

Формат выходного файла

Выведите строку-палиндром, полученную из $S$ путем добавления латинских букв в хвост. Если решений несколько, необходимо вывести любое из них.

Примеры

Входные данные

ABC

Выходные данные

ABCBA

Входные данные

ABCABDABFBAD

Выходные данные

ABCABDABFBADBACBA

#111460

Делимость

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Сыктывкар, 7-9 классы, 2013, Задача A ]

Межгалактический отдел звездных головоломок «МОЗГ» совершил новое открытие. Они изобрели сверхбыстрый алгоритм для нахождения остатка от деления огромного двоичного числа на десятичное. А как известно, любой алгоритм необходимо протестировать. Помогите МОЗГу решить более простую задачу, чтобы сверить ответы.

Вам даны числа. $A$ — большое число в двоичной записи и $B$ — число в десятичной записи, положительное и является степенью двойки.

Вам нужно проверить, делится ли $A$ на $B$ нацело (равен ли нулю остаток от деления).

Формат входного файла

В первой строке дано целое число $A$ в двоичной записи (до 200 цифр).

Во второй строке дано целое число $B$ ($1 \leq B \leq 2*10^9$) в десятичной записи.

Формат выходного файла

YES, если $A$ делится нацело на $B$.

NO в обратном случае.

Примеры

Входные данные

111111010101011010011010100
4

Выходные данные

YES

Входные данные

111111010101011010011010100
16

Выходные данные

NO

#111462

Демократия

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Сыктывкар, 7-9 классы, 2013, Задача E ]

Межгалактический совет обеспокоен недавним внедрением совершенно дурацких и бесполезных межпланетных законов. Как так! Ведь во всем межгалактическом союзе построена непоколебимая демократия. Для принятия какого-либо решения проводится референдум. Каждая планета голосует внутри себя, Если более половины жителей планеты ЗА — то и вся планета ЗА. Далее, если более половины планет ЗА — то решение утверждается. Но ходят слухи, что иногда требуется намного меньше, чем половина всех жителей межгалактического союза, чтобы любое решение было утверждено, чем и пользуются бессовестные политики.

МОЗГу поручена задача высшего приоритета, узнать правдивы ли слухи, а точнее — сколько необходимо человеко-голосов, чтобы утвердить любой закон?

Формат входного файла

В первой строке задано целое число $N$ ($1 \leq N \leq 10^3$) — количество планет.

В следующей $N$ чисел $k_i$ ($0 \leq k_i \leq 10^3$) — количество жителей на $i$-ой планете.

Формат выходного файла

Выведите минимальное количество человеко-голосов, необходимых для принятия межгалактических законов.

Примеры

Входные данные

3
5 7 5

Выходные данные

Страница: 1 Отображать по:

Выбрано

Отменить

Добавить в контест