Темы --> Информатика --> Язык программирования --> Типы данных --> Строки
---> 4 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников --> Муниципальный этап --> Москва
    2007(5 задач)
    2008(5 задач)
    2009(5 задач)
    2010(5 задач)
    2011(5 задач)
    2012(5 задач)
    2013(5 задач)
    2014(5 задач)
Страница: 1 Отображать по:
#723
Метод бутерброда
  
Темы: [Строки]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

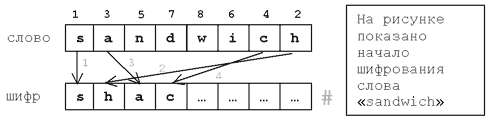
Секретное агентство «Super-Secret-no» решило для шифрования переписки своих сотрудников использовать «метод бутерброда». Сначала буквы слова нумеруются в таком порядке: первая буква получает номер 1, последняя буква - номер 2, вторая – номер 3, предпоследняя – номер 4, потом третья … и так для всех букв (см. рисунок). Затем все буквы записываются в шифр в порядке своих номеров. В конец зашифрованного слова добавляется знак «диез» (#), который  нельзя использовать в сообщениях.

Например, слово «sandwich» зашифруется в «shacnidw#».

 Задача С, рис. 3

К сожалению, программист «Super-Secret-no», написал только программу шифрования и уволился. И теперь агенты не могут понять, что же они написали друг другу. Помогите им.

Входные данные

Вводится слово, зашифрованное методом бутерброда. Длина слова не превышает 20 букв.

Выходные данные

Выведите расшифрованное слово.

Примеры
Входные данные
Aabrrbaacda#
Выходные данные
Abracadabra
#1181
Благозвучное слово
  
Темы: [Строки] [Цикл for]

Все буквы латинского алфавита делятся на гласные и согласные. Гласными буквами являются: a, e, i, o, u, y. Остальные буквы являются согласными.

Слово называется благозвучным, если в этом слове не встречается больше двух согласных букв подряд и не встречается больше двух гласных букв подряд. Например, слова abba, mama, program — благозвучные, а слова aaa, school, search — неблагозвучные.

Вводится слово. Если это слово является неблагозвучным, то разрешается добавлять в любые места этого слова любые буквы. Определите, какое минимальное количество букв можно добавить в это слово, чтобы оно стало благозвучным.

Входные данные

Вводится слово, состоящее только из маленьких латинских букв. Длина слова не превышает 30 символов.

Выходные данные

Выведите минимальное число букв, которые нужно добавить в это слово, чтобы оно стало благозвучным.

Комментарии к примерам тестов

1. Слово уже является благозвучным.

2. Достаточно добавить одну гласную букву, например, между буквами s  и с

Примеры
Входные данные
program
Выходные данные
0
Входные данные
school
Выходные данные
1
#111857
Телефонные номера
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Телефонные номера в адресной книге мобильного телефона имеют один из следующих форматов:

+7<код><номер>

8<код><номер>

<номер>

где <номер> — это семь цифр, а <код> — это три цифры или три цифры в круглых скобках. Если код не указан, то считается, что он равен 495. Кроме того, в записи телефонного номера может стоять знак “-” между любыми двумя цифрами (см. пример).

На данный момент в адресной книге телефона Васи записано всего три телефонных номера, и он хочет записать туда еще один. Но он не может понять, не записан ли уже такой номер в телефонной книге. Помогите ему!

Два телефонных номера совпадают, если у них равны коды и равны номера. Например, +7(916)0123456 и 89160123456 — это один и тот же номер.

Входные данные

В первой строке входных данных записан номер телефона, который Вася хочет добавить в адресную книгу своего телефона. В следующих трех строках записаны три номера телефонов, которые уже находятся в адресной книге телефона Васи.

Гарантируется, что каждая из записей соответствует одному из трех приведенных в условии форматов.

Выходные данные

Для каждого телефонного номера в адресной книге выведите YES (заглавными буквами), если он совпадает с тем телефонным номером, который Вася хочет добавить в адресную книгу или NO (заглавными буквами) в противном случае.

Примеры
Входные данные
8(495)430-23-97
+7-4-9-5-43-023-97
4-3-0-2-3-9-7
8-495-430
Выходные данные
YES
YES
NO
#112831
Строки
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Даны три строки, состоящие из строчных латинских букв. С этими строками можно производить следующие операции: либо заменить один символ строки на два таких же символа (например, заменить символ «a» на «aa»), либо, наоборот, заменить два подряд идущих одинаковых символа на один такой же символ.

Необходимо при помощи этих операций сделать все три строки равными какой-то другой общей строке S либо определить, что это сделать невозможно. При этом нужно минимизировать общее количество операций.

Входные данные

Программа получает на вход три строки, состоящие из строчных букв латинского алфавита. Длина каждой строки не превышает 100 символов.

Выходные данные

Если при помощи указанных операций возможно сделать все три строки равными, выведите такую строку S , что суммарное число операций, необходимых для преобразования всех трёх данных строк к строке S , будет минимальным. Если этого сделать нельзя, программа должна вывести одно слово IMPOSSIBLE (заглавными буквами).

Примечание

Решение, которое выводит правильный ответ только на тестах из условия и тех тестах, на которых ответом является слово IMPOSSIBLE, будет оцениваться в 0 баллов.

Примеры
Входные данные
aaaza
aazzaa
azzza
Выходные данные
aazza
Входные данные
xy
xxyy
yx
Выходные данные
IMPOSSIBLE
Страница: 1 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест