Рано утром Вася решил сделать домашнее задание по информатике. Начать выполнение задания Вася решил с поиска подходящей тетрадки. Добравшись до ящика с чистыми тетрадями, он открыл одну из них. Вася ещё не до конца проснулся и поэтому видит только часть тетрадки и не может сообразить, какая это тетрадка: в клетку, в линейку или в вертикальную линейку. Помогите ему это сделать.
Формально, дана двухмерная таблица из нулей и единиц — часть тетрадки, которую видит Вася. Единицей обозначается закрашенный участок, а нулем — незакрашенный. Назовём вертикальной линией столбец таблицы, все элементы которого — единицы, а горизонтальной линией — строку таблицы, все элементы которой — единицы. Гарантируется, что каждая единица в таблице содержится в какой-либо линии.
Тетрадкой в клетку называется тетрадка, в которой содержатся вертикальные и горизонтальные линии. Тетрадкой в линейку называется тетрадка, в которой содержатся только горизонтальные линии. Тетрадкой в вертикальную линейку называется тетрадка, в которой содержатся только вертикальные линии.
Известно, что в целой тетрадке все расстояния между линиями одинаковы (то есть все клетки — квадраты, все линейки одинаковой ширины). Гарантируется, что линии не могут располагаться рядом (между ними всегда есть промежуток).
Вам требуется написать программу, которая определит тип тетрадки или скажет, что это невозможно однозначно сделать по данной таблице.
В первой строке входных данных даны целые числа n и m (1 ≤ n, m ≤ 1 000) — количество строк и столбцов в таблице. Следующие n строк по m чисел содержат целые числа ai, j (0 ≤ ai, j ≤ 1) — элементы таблицы, задающие видимую часть тетради.
Требуется вывести одну из строк:
- «Square», если заданная тетрадка расчерчена в клетку;
- «Line», если тетрадка расчерчена в линейку;
- «Vertical line», если тетрадка расчерчена в вертикальную линейку;
- «?», если невозможно однозначно определить, к какому типу относится данная тетрадь.
3 5
00100
11111
00100
Square
4 5
11111
00000
11111
00000
Line
5 5
00000
00000
11111
00000
00000
?
В данной задаче баллы за каждый тест начисляются независимо от прохождения остальных тестов и суммируются.
На день рождения Егору подарили волшебный квадрат.
Волшебный квадрат — это таблица 3 × 3, в каждой из ячеек которой находятся числа от 0 до 9. Егор придумал следующую игру с волшебным квадратом: он загадывает число N и пытается так поставить числа в каждую ячейку квадрата, чтобы сумма чисел в каждой строке и каждом столбце была равна в точности N.
Пусть расстановка — это волшебный квадрат, заполненный числами. Тогда расстановки A и B считаются различными, если хотя бы для каких-то строки x и столбца y выполняется неравенство Ax, y ≠ Bx, y, где Ax, y и Bx, y — это числа, находящиеся в строке x и столбце y в расстановках A и B соответственно.
Егор задумался, сколько всего существует различных расстановок таких, что сумма в каждой строке и в каждом столбце была равна в точности N.
Напишите программу, которая поможет ответить на вопрос Егора.
Единственная строка входных данных содержит целое число N (0 ≤ N ≤ 109).
Требуется вывести одно число — искомое количество расстановок.
0
1
В примере из условия существует всего одна допустимая расстановка — это таблица 3 × 3, состоящая из нулей. Очевидно, что сумма элементов в любой строке или столбце в такой расстановке равна 0.
В одном известном всем городе скоро стартуют Зимние Олимпийские игры. В связи с этим организаторы игр решили провести эстафету Олимпийского огня — самую продолжительную и масштабную в истории Олимпийских игр. Эстафета состоит из N этапов, каждый длиной ai километров (1 ≤ i ≤ N). У организаторов имеется бесконечное количество олимпийских факелов, каждый из которых может непрерывно гореть на протяжении K километров забега. По правилам эстафеты каждый факел используется только один раз. В начале каждого этапа участникам эстафеты выдаётся некоторое число факелов, такое, чтобы олимпийский огонь удалось донести до конца этапа. По окончании этапа все использованные (полностью или частично) факелы передаются в дар своим факелоносцам.
В процессе подготовки эстафеты выяснилось, что последовательно идущие этапы можно объединить в один этап, и таким образом на проведение эстафеты потребуется меньше факелов. Однако по соображениям техники безопасности нельзя объединять больше, чем M подряд идущих этапов.
Напишите программу, которая по известной схеме эстафеты Олимпийского огня определяет, какое максимальное число факелов можно «сэкономить» и какие этапы для этого нужно объединить.
В первой строке заданы 3 натуральных числа N, M и K (N ≤ 106, M ≤ 10, K ≤ 108).
Во второй строке заданы N натуральных чисел ai (ai ≤ 109).
В первой строке выведите одно натуральное число F — на сколько можно максимально сократить количество используемых факелов на протяжении всей эстафеты.
Во второй строке выведите одно натуральное число P — количество групп объединённых этапов.
Затем в P строках выведите сами группы — по 2 натуральных числа si и ci, где si — номер первого этапа в группе, а ci — количество этапов в группе. Все si должны идти в порядке возрастания, а ci не превосходить M. Если существует несколько оптимальных решений, разрешается вывести любое.
5 3 3
1 1 1 3 3
2
1
1 3
6 3 3
1 1 1 1 1 1
4
2
1 3
4 3
5 5 2
2 4 6 8 10
0
0
«Sam Topge был найден мертвым в своей квартире» — большими буквами было написано на обложке местной газетки, которую так любил читать дома по вечерам Мистер Холмс. "Уже четвертый иностранец за месяц", — грустно подумал он. — "Завтра будет много работы". Холмс выключил свет и, повалившись на кровать от усталости, сладко уснул.
Мистер Холмс работает детективом, и, конечно же, именно ему поручено исследовать дело об этом серийном убийце. "Никаких улик, никаких следов борьбы. Как тут вообще что-то можно найти? Даже медики не могут определить, как они умерли", — думал он, сидя на работе. Никакой зацепки не было, можно было надеяться только на чудо.
Проведя весь день на работе, безуспешно пытаясь найти хоть какую-нибудь маленькую улику, мистер Холмс, грустный и уставший, потопал домой. Шел он, как обычно, через лавку с газетами, чтобы купить свежий выпуск его любимой газеты. "Здравствуйте, Чед, мне как обычно" — "Вы выглядите неважно, мистер Холмс. Возьмите отпуск, отдохните. Вот, держите газету". "Спасибо за совет", — ответил Холмс, взял газету и побрел домой.
Поужинав, Холмс сел на свое любимое кресло перед камином, и, достав свою любимую газету, расслабился после тяжелого рабочего дня. "Что-то не так", — подумал он, увидев в своей привычной газете другой шрифт и формат текста. Он почувствовал, что и бумага недостаточно мягкая, как полагается его любимой газете. "Что мне подсунули? Это не та газета!" — снова напрягся Холмс. "«Stopgame». Ну что за заголовок? Что это за странная газета? Ненавижу этот день!". Холмс бросил газету в камин, и отправился спать.
Под утро у детектива не вылетало из головы название газеты. "Stopgame... Stopgame... Как будто я уже недавно это где-то видел..." — думал он, идя на работу.
"Точно!" — громко воскликнул Холмс в полицейском участке, чем привлек внимание всех вокруг. Детектив быстро взял какую-то бумажку, написал на ней «Stopgame», порвал ее на несколько частей и сложил их. "Sam Topge", — обрадовался Холмс. — "Но почему? Может, это случайность?". Детектив выскочил из участка и побежал к продавцу газет.
"Вы мне вчера дали не ту газету!" — запыхавшись, сказал Холмс — "Дайте мне такую же, пожалуйста, на ней написано «Stopgame»". Чед хотел было извиниться, но, видя сияющие глаза Холмса, понял, что, кажется, он ему только помог. Чед протянул Холмсу газету, тот выхватил ее из рук и принялся спешно читать ее.
"Какая-то статья про зависимых от компьютерных игр детей... Ничего интересного. Может, просто совпадение?" — подумал Холмс, взял газету, и пошел обратно в офис.
Перечитав газету, Холмс не нашел ничего интересного. Посмотрел данные о самой газете — уже более десяти лет она продается в ближайших районах. Потеряв надежду, Холмс отбросил газету на дальний край своего стола и принялся снова искать зацепки.
Прошло еще 3 дня. Холмс потерян. "Их убивает что-то изнутри. Что-то просто отнимает у них жизнь. И уже довольно скоро появится новая жертва. Все они умирают вечером, все во вторник. А завтра вторник. Нужно срочно что-то делать". Холмс увидел отброшенную газету, и его посетила одна гениальная мысль.
Холмс рванул в дома, где жили иностранцы. У каждого из них он нашел эту газету последнего выпуска, которую еще могли купить убитые. "Бинго! Зацепка!" — возрадовался Холмс. — "Имя каждого из убитых — подпоследовательность букв из заголовка газеты!". "Кто же это мог быть? Как эти имена так удивительно могут образовывать другие слова?". Холмс решил проверить сотрудников редакции газеты. Оказалось, главный по заголовкам в последнее время работает на дому. "Мы его видели за странным делом", — говорят сотрудники, — "он нарезал бумагу и клеил в странную кожаную потертую тетрадку".
Холмс работал всю ночь напролет. Он выяснил, кто этот сотрудник, и узнал, что всех этих иностранцев он знал — они вместе воевали. Под утро Холмс решил навестить его. Но не тут-то было: его не было дома.
Газета выходила каждый вторник утром. Холмс решил сходить за ней. Взяв газету, он передал ее своему напарнику, а сам решил выяснить, кто может быть следующей жертвой. Холмс, всю ночь провозившись с делом странного сотрудника редакции газеты, быстро справился с этой задачей, после чего раздался громкий звонок телефона Холмса.
"Он в своем доме, делает что-то странное", — сообщили ему коллеги. И тут Холмс понял, что у него совсем мало времени. Но Холмс хочет знать точно, сколько времени убийца потратит на разрезание названия газеты. "Эй, Ватсон, посчитай мне быстро, сколько разрезов ему нужно сделать, чтобы собрать имя и фамилию убитого?" Сегодня Ватсон — это вы. Помогите Холмсу определить минимальное количество времени, которое уйдет у убийцы на разрезание названия газеты.
Длину строки q обозначим как |q| (|abac| = 4, |sam| = 3). Во входном файле содержатся 3 строки s, t1, t2 (|s| = |t1| + |t2|, 1 ≤ |t1|, |t2| ≤ 1 000). Все строки содержат только маленькие латинские буквы.
Подстрокой p[l, r] назовем строку, состоящую из символов pl, pl + 1, ..., pr - 1, pr, где pi — i-тый символ строки p («cde» является подстрокой строки «abcdef», «bcf» — не является).
Тогда любую строку p можно представить в виде разбиения на непересекающиеся подстроки p[x0 + 1, x1] + p[x1 + 1, x2] + p[x2 + 1, x3] + ... + p[xn - 1 + 1, xn], где 0 = x0 < x1 < x2 < ... < xn - 1 < xn = |p|. При этом длиной разбиения будем называть количество чисел xi, то есть число n.
В данной задаче требуется найти разбиение строки s такое, чтобы из получившихся подстрок можно было сложить строки t1 и t2, не нарушая порядка, в котором подстроки шли в исходной строке. Например, из строки «adbc» нельзя будет выложить слова «cad» и «b», так как порядок подстрок «ad» и «c» будет нарушен.
Программа должна выдавать на экран одно число — минимально возможную длину такого разбиения, то есть количество разрезов, которые потребуется сделать убийце.
Гарантируется, что существует разбиение строки s хотя бы одним способом, чтобы получились строки t1 и t2.
stopgame
sam
topge
3
ababbaba
abbb
abaa
4
В первом примере из условия строку можно разрезать следующим образом: stopgame  s|topg|am|e.
s|topg|am|e.
Во втором примере: ababbaba  ab|abb|a|b|a.
ab|abb|a|b|a.
Сегодня в длительной и непримиримой войне между Аарляндией и Берляндией происходит ключевая битва. Командование армии Берляндии собралось в штабе перед специальным радаром, чтобы следить за сражением. Радар показывает неуничтоженные боевые единицы (и их координаты), которые в данный момент находятся на поле боя.
К сожалению, радар этот не очень хорош. Боевые единицы на нем могут исчезать и появляться вновь на том же месте. К тому же, радар не показывает принадлежность боевых единиц армиям (то есть непонятно, свой ли это солдат или чужой). Командование знает порядок событий вида:
- боевая единица возникла на радаре в точке (x, y);
- боевая единица исчезла с радара из точки (x, y).
В общей неразберихе боя командование армии Берляндии с помощью радара иногда пытается понять, где в данный момент находится линия фронта (это нужно для планирования дальнейших боевых действий). Исходя из соображения о том, что силы примерно равны, командование полагает, что линия фронта — это вертикальная прямая вида 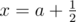 (a — неотрицательное целое число), такая, что количество боевых единиц слева от этой прямой строго равно количеству боевых единиц справа от этой прямой, и a максимально (то есть, если возможных линий фронта существует несколько, руководство хочет знать самую правую из них).
(a — неотрицательное целое число), такая, что количество боевых единиц слева от этой прямой строго равно количеству боевых единиц справа от этой прямой, и a максимально (то есть, если возможных линий фронта существует несколько, руководство хочет знать самую правую из них).
Помогите командованию армии не проиграть эту битву. Напишите программу, которая будет сообщать линию фронта для текущей ситуации на поле боя, когда этого требует руководство армии Берляндии.
В первой строке вводится одно целое число n — количество событий (1 ≤ n ≤ 106).
В следующих n строках вводятся описания событий трех видов.
- «A x y» — боевая единица возникла на радаре в точке с целочисленными координатами x, y (1 ≤ x, y ≤ 109).
- «D x y» — боевая единица исчезла с радара из точки с целочисленными координатами x, y (1 ≤ x, y ≤ 109). Гарантируется, что до этого запроса в этой точке на радаре была боевая единица.
- «Q» — командование Берляндии захотело узнать текущую линию фронта.
Для каждого события вида «Q» выведите в отдельной строке максимальное неотрицательное целое a такое, что прямая 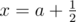 — это линия фронта. В случае, если линии фронта не существует, или существует бесконечно много вариантов провести линию фронта, выведите «-1».
— это линия фронта. В случае, если линии фронта не существует, или существует бесконечно много вариантов провести линию фронта, выведите «-1».
12
A 1 1
A 2 1
Q
A 2 2
A 3 1
Q
A 4 1
A 5 1
Q
D 1 1
D 5 1
Q
1
-1
2
2
- Решения, корректно работающие при x, y ≤ 10, будут оцениваться не менее чем 32 баллами.
- Решения, корректно работающие при x, y ≤ 100, будут оцениваться не менее чем 44 баллами.
- Решения, корректно работающие при x, y ≤ 1 000 000, будут оцениваться не менее чем 80 баллами.