#3854

Fruit Slice

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Интернет этап, 2011, Задача A ]

Правила игры Fruit Slice для сенсорных мобильных телефонов очень просты. В течение некоторого времени на экране появляются фрукты, а игрок должен провести пальцем по экрану так, чтобы линии, проведенные им, пересекли как можно больше фруктов. В случае, если линия пересекает фрукт, он разрезается на две половинки, а игрок получает очки следующим образом:

за разрезание большого фрукта игрок получает два очка, за разрезание маленького — три;
если одной линией игрок разрезал три фрукта, то помимо очков, полученных за каждый фрукт по отдельности, он получает еще 5 бонусных очков;
если одной линией игрок разрезал 4 и более фруктов, то помимо очков, полученных за каждый фрукт по отдельности, он получает еще 10 бонусных очков.

Вася поиграл в игру и набрал суммарно P очков, при этом N раз получив 5 бонусных очков и M раз получив 10 бонусных очков. Теперь ему интересно, какое минимальное количество фруктов можно разрезать согласно правилам этой игры, чтобы добиться такого же результата.

Входные данные

В единственной строке вводятся три числа P, N и M (0 ≤ P ≤ 10⁹, 0 ≤ N, M ≤ 10⁶).

Выходные данные

Выведите одно число — минимальное количество фруктов, которое нужно разрезать, чтобы добиться указанного результата. Гарантируется, что входные данные корректны, то есть существует такой набор фруктов, что возможно набрать суммарно P очков, при этом N раз получив 5 бонусных очков и M раз получив 10 бонусных очков.

Примечание

В первом примере добиться указанного результата можно, разрезав 5 маленьких фруктов и 1 большой. При этом у игрока есть возможность получить 5 бонусных очков, разрезав какие-то три фрукта одной линией.

Во втором примере добиться указанного результата можно, разрезав одной линией 3 больших фрукта и 1 маленький. Обратите внимание, что поскольку Вася один раз получил 10 бонусных очков, он не может добиться указанного результата, разрезав менее 4-х фруктов.

Система оценки

Тесты в этой задаче разбиты на группы. Баллы начисляются только за группу целиком в том случае, когда пройдены все тесты группы, а также все тесты предыдущих групп.

Тесты 1–2. Тесты из условия, оцениваются в 0 баллов.
Тесты 3–5. $P \le 30$, $N, M \le 1$, оцениваются в 30 баллов.
Тесты 6–9. $P \le 10^7$, оцениваются в 30 баллов.
Тесты 10–12. Дополнительных ограничений нет, оцениваются в 40 баллов.

Примеры

Входные данные

22 1 0

Выходные данные

Входные данные

19 0 1

Выходные данные

#3855

Ожерелье

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Интернет этап, 2011, Задача B ]

Дано ожерелье, состоящее из n красных или черных бусин, нанизанных на нить. Ожерелье представляет собой замкнутую окружность. Разрежем ожерелье на 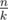$\text{[math]}$ связных цепочек по k бусин. Требуется написать программу, которая вычислит максимальное количество цепочек, состоящих только из красных бусин, которое можно получить среди всех способов разрезать ожерелье.

Входные данные

В первой строке входных данных содержатся два натуральных числа n и k, не превышающие 10⁶. Гарантируется, что k является делителем числа n. Во второй строке даны n чисел, разделенных одним проблеом, каждое из которых равно 0 или 1. i-ое число в этой последовательности обозначает цвет i-ой бусины в порядке обхода по часовой стрелке: 0 — черный, а 1 — красный, соответственно.

Выходные данные

В выходной файл выведите максимальное количество цепочек, состоящих из k красных бусин, которое возможно получить.

Примечание

Гарантируется, что решения, корректно работающие при ограничении N ≤ 10 000, будут оцениваться из 60 баллов.

Примеры

Входные данные

9 3
1 1 1 1 0 0 0 1 1

Выходные данные

Входные данные

9 3
0 1 1 1 1 0 1 1 1

Выходные данные

#3856

Короли

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Интернет этап, 2011, Задача C ]

Дано прямоугольное шахматное поле размером n × m клеток (n столбцов, m строк), на котором находятся два короля. Для каждого короля даны его начальные координаты (x, y) и начальный вектор скорости (v_x, v_y). Числа v_x и v_y обозначают, что за один ход фигура передвигается на v_x клеток по горизонтали и на v_y по верткали, при этом числа v_x и v_y могут принимать значения - 1, 0 и 1. Короли по очереди делают ходы в направлении своих векторов скоростей, меняя направления у стенок доски по закону отражения (при отражении от края доски одна из компонент скорости меняется, при отражении от угла меняются обе компоненты скорости). Если король после очередного хода попадает на клетку с королём противника, то он объявляется победителем и игра заканчивается. Первым ходит белый король.

Требуется определить, закончится ли игра и, в случае положительного ответа, кто из королей и на каком ходу выиграет.

Входные данные

В первой строке входного файла даны натуральные числа n и m (1 ≤ n, m ≤ 10⁶). Во второй строке находятся четыре целых числа x_w, y_w, v_x, w, v_y, w, задающие начальное положение и вестор скорости белого короля. В третьей строке даны четыре целых числа, x_b, y_b, v_x, b, v_y, b, задающие начальное положение и вектор скорости чёрного короля. Гарантируется, что 1 ≤ x_w, x_b ≤ n, 1 ≤ y_w, y_b ≤ m, - 1 ≤ v_x, w, v_y, w, v_x, b, v_y, b ≤ 1. Кроме того, гарантируется, что короли не могут иметь нулевой вектор скорости (обе компоненты не могут быть одноременно равны 0).

Выходные данные

В случае, если игра не закончится, в выходной файл следует выдать единственную строку «TIE». Если же игра закончится после k-го хода одного из королей, программа должна выдать строку, содержащую «WHITE k» или «BLACK k».

Примечание

Решения, корректно работающие при 1 ≤ n, m ≤ 50, будут набирать не менее 20 баллов. Решения, корректно работающие при 1 ≤ n, m ≤ 1000, будут набирать не менее 50 баллов.

Примеры

Входные данные

3 3
1 2 1 1
2 1 1 1

Выходные данные

WHITE 2

Входные данные

3 3
1 1 1 1
3 1 1 1

Выходные данные

BLACK 1

#3857

Головоломка

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Интернет этап, 2011, Задача D ]

Картина в голове Штирлица не складывалась. За год из Центра поступило N · M фрагментов нового задания. Штирлиц запомнил каждый фрагмент и теперь складывает из них целое сообщение.

Текст задания записан на клетчатой прямоугольной странице размера (5N) × (5M), который разрезан на N · M частей. Каждый фрагмент сообщения можно представить квадратом 5 × 5 (серые клетки), у которого с каждого краю (заштрихованные области) может быть только один «выступ» или «впадина». Обратите внимание, что к краям не относятся углы квадрата (см. иллюстрацию).

Более формально, каждый фрагмент можно представить в виде фигуры, которая получена из левой части иллюстрации, изменением цвета не более чем одной клетки из каждой заштрихованной области.

$\text{[math]}$

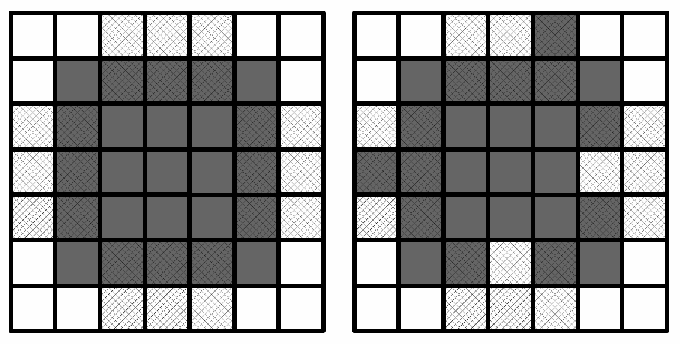
Фрагмент может иметь ровную сторону (т.е. не имеет выступа или впадины) только если соответствующая сторона фрагмента является границей сообщения.

Требуется написать программу, которая поможет Штирлицу собрать из фрагментов целое сообщение.

Входные данные

В первой строке входных данных даются размеры сообщения — натуральные числа N и M (1 ≤ N ≤ 5, 1 ≤ M ≤ 4).

В следующих 7 · N · M строках по 7 символов задаются фрагменты сообщения. Каждый фрагмент состоит из 7 строк. Пустая часть фрагмента задается символами «.», а часть фрагмента, содержащая текст, символами «#».

Выходные данные

Выведите 7 · N строк по 7 · M символов, задающих как надо разложить части, чтобы получить целое сообщение. Части сообщения можно совмещать только параллельным переносом (то есть, запрещается поворачивать и переворачивать фрагменты сообщения).

Примечание

Если существует несколько способов восстановить сообщение, требуется вывести любой из них. Решения, корректно работающие при ограничениях N · M ≤ 10, оцениваются в 50 баллов.

Примеры

Входные данные

1 2
.......
.#####.
.#####.
.####..
.#####.
.#####.
.......
.......
.#####.
.#####.
######.
.#####.
.#####.
.......

Выходные данные

..............
.#####..#####.
.#####..#####.
.####..######.
.#####..#####.
.#####..#####.
..............

#111476

Последовательность (В)

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Московская область, Интернет этап, 2010, Задача A ]

Мальчику Пете очень нравится математика. Недавно он выписал открыл новую последовательность чисел и, назвав её в свою честь, тут же записал её на длинной ленте, чтобы не забыть. Всё бы хорошо, но у Пети есть младший брат Гена. Гене не очень нравится математика - он мечтает стать дизайнером. Вот и сейчас, увидев новую красивую ленточку, он решил вырезать её часть и украсить ей свою комнату. А чтобы украшению порадовался и Петя, Гена решил вырезать такую часть, чтобы сумма всех чисел на ней была бы как можно больше.

Входные данные

В первой строке входного файла записано число n (1 ≤ n ≤ 100000) - длина последовательности Пети. Во второй строке записаны числа a₁, ..., a_n - сама последовательность( - 10⁹ ≤ a_i ≤ 10⁹).

Выходные данные

Выходной файл должен содержать два числа - максимальную сумму, которую может получить Гена, и количество вариантов получить данную сумму.

Примеры

Входные данные

5
-1 2 3 -2 2

Выходные данные

5 2