Крупная межгалактическая сеть мебельных магазинов Galactic-Мебель недавно вышла на рынок мебели для кухонь в звездной системе LoST-2007. В этой звездной системе во всех квартирах кухни имеют форму прямоугольника размером a на b метров. При этом вдоль одной из стен принято ставить стол, в смежной с ней стене находится окно. Таким образом, для размещения различных кухонных шкафчиков остается угол со сторонами a и b метров.
Для экономии места в этой звездной системе принято ставить шкафчики вплотную друг к другу и к углу кухни. Кроме этого, сами шкафчики встраиваются внутрь стены, то есть вдоль стены расположены только их дверцы.
В звездной системе LoST-2007 используется n типов кухонных шкафчиков. Каждый тип шкафчиков характеризуется своей шириной wi, при этом на кухне должен присутствовать ровно один экземпляр каждого типа шкафчиков.
Недавно директор маркетингового отдела Galactic-Мебель заметил, что он может предложить клиентам несколько вариантов расположения шкафчиков на кухне. Различными считаются варианты, которые отличаются расположением хотя бы одного шкафчика. При этом шкафчики различных типов могут иметь одинаковую ширину, однако отличаются внешней отделкой. Так что даже размещения, которые отличаются лишь позициями шкафчиков с равной шириной, считаются различными.
Например, пусть a = 3, b = 4 и есть два типа шкафчиков, шириной 1 и 2, соответственно.
Первая строка входного файла содержит три целых числа: \(a\), \(b\) и \(n\) (1 ≤ \(a\) ≤ 300, 1 ≤ \(b\) ≤ 300, 1 ≤ \(n\) ≤ 100). Каждая из следующих \(n\) строк содержит целое число \(w_i\) (1 ≤ \(w_i\) ≤ 300) — ширину соответствующего шкафчика.
Выведите в выходной файл количество различных планировок кухни.
7 5 3 1 2 3
18
1 6 2 3 2
2
3 8 3 2 4 5
0
22 21 5 20 3 4 5 6
48
Рассмотрим прямоугольную таблицу размером n m. Занумеруем строки таблицы числами от 1 до n, а столбцы – числами от 1 до m. Будем такую таблицу последовательно заполнять числами следующим образом.
Обозначим через aij число, стоящее на пересечении i-ой строки и j-ого столбца. Первая строка таблицы заполняется заданными числами – a11, a12, …, a1m. Затем заполняются строки с номерами от 2 до n. Число aij вычисляется как сумма всех чисел таблицы, находящихся в «треугольнике» над элементом aij. Все вычисления при этом выполняются по модулю r.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ai,j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Более точно, значение aij вычисляется по следующей формуле:
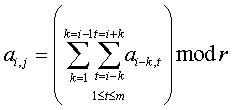
Например, если таблица состоит из трех строк и четырех столбцов, и первая строка состоит из чисел 2,3,4,5, а r = 40 то для этих исходных данных таблица будет выглядеть следующим образом (взятие по модулю показано только там, где оно приводит к изменению числа):
| 2 | 3 | 4 | 5 |
| 5 = 2 + 3 | 9 = 2 + 3 + 4 | 12 = 3 + 4 + 5 | 9 = 4 + 5 |
| 23 = 2 + 3 + 4 + 5 + 9 | 0 = (2 + 3 + 4 + 5 + 5 + 9 + 12) mod 40 = 40 mod 40 | 4 = (2 + 3 + 4 + 5 + 9 + 12 + 9) mod 40 = 44 mod 40 | 33 = 3 + 4 + 5 + 12 + 9 |
Требуется написать программу, которая по заданной первой строке таблицы (a11, a12, …, a1m), вычисляет последнюю строку, как описано выше.
Первая строка входного файла содержит числа n, m и r (2 ≤ n, m ≤ 2000, 2 ≤ r ≤ 109) – число строк и столбцов таблицы соответственно, а так же число, по модулю которого надо посчитать ответ. Следующая строка содержит m целых чисел – первую строку таблицы: a11, a12, …, a1m. Все a1i неотрицательны и не превосходят 109.
В первой строке выходного файла необходимо вывести m чисел – последнюю строку таблицы: an1, an2, …, anm.
2 3 10 1 2 3
3 6 5
3 3 10 1 1 1
8 0 8
3 4 40 2 3 4 5
23 0 4 33